Fractions Minus the Friction. A guide to four teaching practices

Introduction

Understanding fractions has a significant impact on both individuals and society. Fractions are an integral part of everyday life, from performing various job tasks to making healthy-living choices and managing personal finances. Unfortunately, many adults struggle with basic fraction concepts and procedures. These challenges often begin in primary school and can persist through secondary school. However, there is a growing body of research that offers valuable insights into how to effectively teach and learn fractions. The purpose of this guide is to describe the importance of learning fractions and present four research-informed instructional strategies to enhance fraction teaching and learning.

Importance of learning fractions

What are fractions?

Mathematically speaking, fractions are rational numbers that represent a part of a whole that is partitioned into equal parts. The whole can be defined as a single object (e.g., a pizza), a set of objects (e.g., a box of biscuits), a specific length (e.g., a kilometre), a specific volume (e.g., a litre), or other representations. Fractions are symbolically expressed by a numerator to denote the number of equal parts being counted and a denominator to denote the total number of equal parts in the whole. For example, 2/5 represents the quantity of two equal parts of a whole that is partitioned into five equal parts.

Why are fractions important?

Understanding fractions lays the groundwork for success in advanced mathematics and science. Fraction knowledge uniquely predicts students’ performance in algebra, even more than their knowledge of whole numbers (Bailey et al., 2012; Booth & Newton, 2012; Cirino et al., 2022; Viegut, Stephens, & Matthews, 2024). Booth and Newton (2012) found that students’ ability to place unit fractions on a number line is a key algebra readiness skill, as it is linked to understanding features of algebraic equations (like the equal sign, negative sign, variables), solving equations, and working with word problems. Similarly, the ability to place non-unit fractions on a number line connects to solving algebraic equations, likely because it builds on students’ proportional reasoning skills.

Since fraction knowledge is a unique predictor of success in Algebra 1, which is considered a gateway to advanced mathematics in secondary school (e.g., advanced secondary algebra), building strong fraction skills is crucial (Siegler et al., 2012). Tyson and Roksa (2017) found that success in Algebra 1, particularly in rigorous courses, increases students’ likelihood of succeeding in higher-level maths (e.g., Algebra 2). This, in turn, has a positive impact on higher education  and career outcomes (Gaertner, Kim, DesJardins, & McClarty, 2014). Overall, these findings highlight the pivotal role of fractions in advancing students’ maths proficiency and underscore the importance of developing a strong understanding of fractions in upper primary and early secondary school.

What are important fraction concepts?

When students begin to study fractions, it is often their first exposure to number systems beyond whole numbers (see Figure 1). As such, students begin to learn that some properties and concepts that they learned in relation to whole numbers do not apply to all real numbers — which include rational and irrational numbers (see section 2.4 for examples).

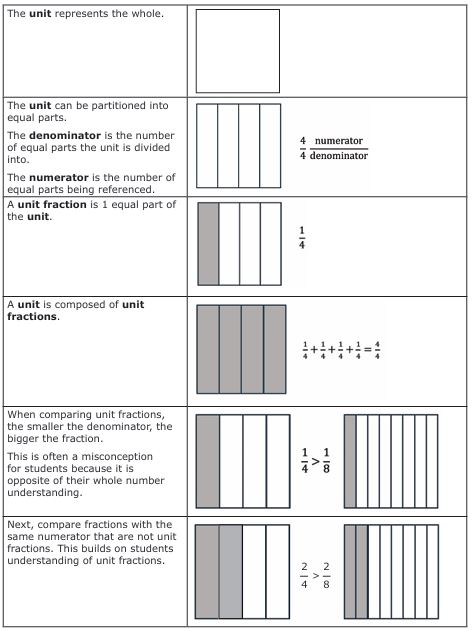
There are three important concepts students learn as they deepen their understanding of fractions: magnitude, equivalence, and density. Applying these concepts to fractions is often students’ first exposure to how concepts and operations differ across number systems.

Understanding fraction magnitude means that students understand that fractions represent a unique quantity, and that quantity can be ordered, compared, and represented on a number line. When applied to fractions, equivalence means knowing that a fraction can be symbolically represented in a variety of equivalent ways but still represents the same quantity. Fraction density refers to the fact that a quantity can be partitioned into infinitely smaller parts.

Text  box 1: A deeper dive into fraction magnitude, equivalence, and density

Magnitude is a concept that applies to all numbers, but it can be especially challenging for students to grasp when learning fractions. Simply put, magnitude is the idea that a number represents a quantity that can be ordered and placed on a number line as a distance from zero (Siegler et al., 2011). When learning whole numbers, students from an early age can link numerals to quantities (e.g., ‘3’ can be represented as three objects). With instruction, they then deepen their understanding by placing whole numbers on a number line. However, when learning fractions, students often do not see fractions as numbers with magnitude. Instead, they may interpret the numerator and the denominator as separate numbers without understanding that a fraction represents the relationship between the numerator and the denominator. This relationship forms a single quantity that can be ordered and represented on a number line as a distance from zero.

The mathematical concept of equivalence is demonstrated in many ways. For example, students learn that the equal sign indicates a relationship between the quantities where both sides have the same value (e.g., 3 + 8 is the same as 0 + 11). When learning fractions, students understand equivalence when they learn that fractions can be symbolically represented in many ways while keeping the same magnitude (e.g., 2/3 = 4/6 = 8/12 = 16/24 = 32/48 and so on). Students often build an understanding of equivalent fractions when working with common or ‘benchmark’ fractions. For example, when students are shown that half of a whole that is partitioned into 10 parts is 5 parts, and can represent this as ½ = 5/10. As their understanding grows, they can begin to use multiplicative reasoning to find equivalent fractions. Procedurally, students can calculate equivalent fractions and understand the correctness of the procedure when they are able to multiply fractions and apply their understanding of the identity property of division (that any number divided by itself is 1) and the identity property of multiplication (that any number multiplied by 1 is that number):

which is the same as

which is the same as

Students understand fraction density when they grasp that a whole can be partitioned into infinitely smaller parts. This concept ties into their understanding of place value and decimals, and represents a unique shift in their understanding of counting. When learning whole numbers, students use a counting sequence to establish a total of objects (e.g., 0, 1, 2, 3). The counting sequence itself also demonstrates that whole numbers have a unique successor (e.g., the unique successor of 2 is 3). When students are first exposed to fractions, they must understand that numbers — namely, fractions — exist between two whole numbers (e.g., ¼, ½ and ¾ are between 0 and 1). Then, they learn that there are numbers that exist between fractions (e.g., ½ is between 2/5 and 3/5). Over time, they recognise that fractions do not behave like whole numbers because they do not have a unique successor. As their knowledge deepens, they can start to see that the number line can be infinitely partitioned into smaller and smaller parts without end (see Figure 7 for an illustration).

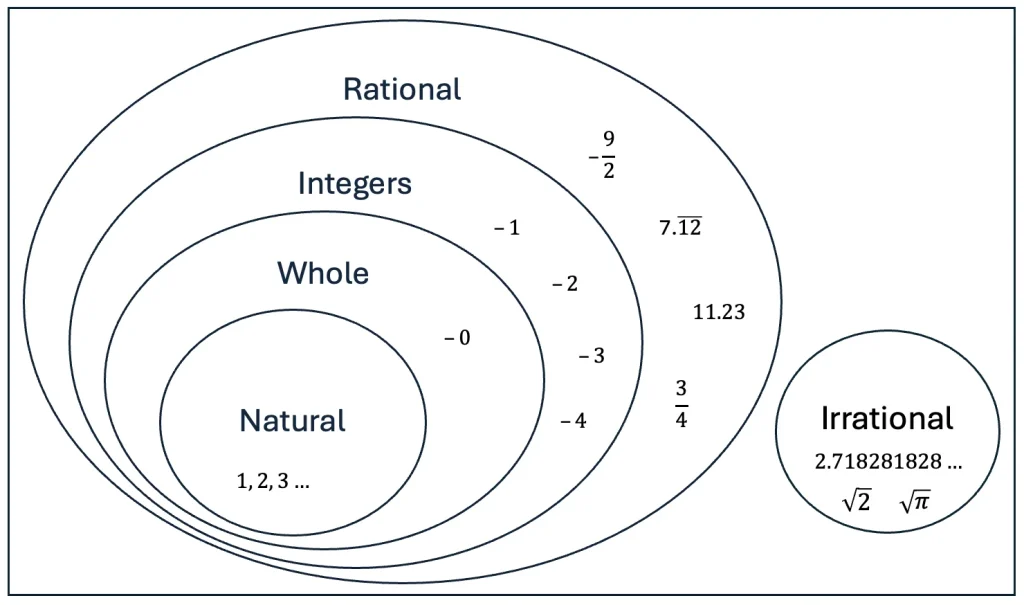
Figure 1. Real numbers (Ketterlin-Geller & Chard, 2011)

To support teachers in implementing key fraction concepts and skills in the classroom, this guide begins with Practice 1, which outlines the learning progression that supports students’ development of fraction proficiency. Practice 2 focuses on designing fraction instruction that is coherent across grades and aligned with other mathematics concepts, like whole numbers. Practice 3 explores the relationship between conceptual understanding and procedural fluency, emphasising the importance of making explicit connections for students. Lastly, Practice 4 addresses common errors and misconceptions that can arise if students’ understanding of fractions is not systematically developed over time.

Each practice includes a description of the approach, the research that supports it, and practical guidance for implementation in the classroom. Throughout the guide, several themes emerge. First, we emphasise the power of using the number line to teach fractions. Second, we reinforce the recommendation by Powell, King, and Benz (2023) to implement systematic and explicit instruction while judiciously incorporating multiple representations — concrete, semi-concrete, and abstract — during instruction. Finally, we stress the importance of carefully planning instruction within and across grades. Effective planning includes:

1. following a learning progression for teaching fraction concepts
2. building on students’ knowledge of whole numbers to deepen their understanding of fraction concepts, especially magnitude
3. fostering both conceptual understanding and procedural fluency, and
4. integrating different instructional models, such as area, length, and set models.

Practice 1: Design instruction along a learning progression

What is this practice?

Learning progressions describe how students develop proficiency in a subject by moving from novice to more sophisticated understanding. They outline the phases or levels through which students build knowledge, develop skills, and deepen their thinking about a topic. These progressions focus not only on concepts and procedures but also on how students process information, such as reasoning and problem-solving strategies.

Given the complexity of fractions, instruction needs to follow a clear progression, with each phase or level of learning well-defined. Each phase should articulate the essential concepts and skills students need to understand, with each building on the next to deepen students’ proficiency. The essential concepts when learning fractions include conceptually understanding magnitude, equivalence, and density, and key skills include procedural fluency in applying the four operations.

What is the research?

Researchers have proposed learning progressions to describe how students develop proficiency in fraction concepts and procedures (see Confrey, 2018, for a comprehensive list of mathematics learning progressions across domains); however, it is important to note that research validating these learning progressions is still emerging.

Here, we focus on the value of learning progressions as tools to help teachers design and sequence instruction. The learning progression described below should not be viewed as a linear sequence in which students must master one phase before moving on to the next. Instead, teachers can integrate key concepts and skills across phases to build on students’ prior knowledge, thereby helping students develop a robust understanding of fraction concepts and skills. Moreover, the phases of learning should be integrated with the Australian Curriculum to ensure that students are meeting the learning expectations specified by the Australian Curriculum, Assessment and Reporting Authority (ACARA; see Text Box for a summary of the development of fraction proficiency specified in the curriculum framework).

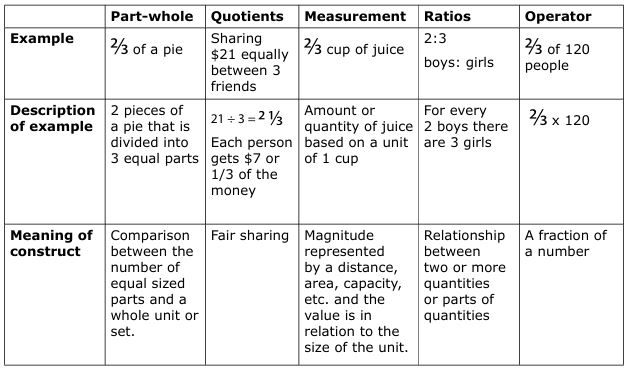
In a recent review of this research, Wellberg, Briggs, and Student (2023) identified five phases or levels of learning that progress from early understandings in primary school to more advanced knowledge in secondary. These levels include part-whole relationships, fractions as quotients or fair-shares, measurement, fractions as ratios or rates, and fractions as operators. We define each of these phases or levels below.

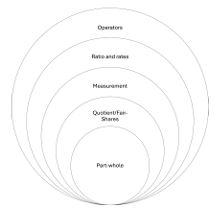
Prior to formal instruction on fractions, many students develop initial fraction understanding through experiences sharing objects and reasoning about proportional relationships (Siegler et al., 2021). For example, young children can share a set of objects (such as candies or balls) equally among a group of people. Similarly, from an early age, students can recognize proportional relationships when expressed in non-symbolic ways such as with geometric figures or through story contexts. These emerging understandings serve as a basis for formal instruction on fractions and can be integrated across the phases of the learning progression.

Students are often formally introduced to fractions through the part-whole model, in which they learn that a fraction represents a partition (the numerator) of a given whole (the denominator). Students recognise that when the unit fraction is the same size, the fraction with a larger numerator is composed of more fractional units.

While this model provides an important link to thinking about fractions as ratios of two integers, or whole numbers, concern has been raised about the part-whole model being incomplete (e.g., lacking a focus on magnitude), causing misconceptions (e.g., imprecise partitioning of a whole), and having limited utility (e.g., interpreting negative fractions, modeling fractions with large denominators) (Siegler et al., 2011). These insufficiencies underscore the importance of advancing students’ understanding along the learning progression.

As students’ understanding deepens, they begin to see fractions as fair-shares or quotients, where a whole is divided into equal parts — a concept tied to fair sharing, which often develops early through students’ informal experiences. Students learn that partitioning a whole into more parts results in smaller shares. This idea helps build students’ understanding of the density principle, emphasising that a quantity can be infinitely divided. Symbolically, students understand that fractions with larger denominators are divided into more, smaller parts.

In both levels, students are beginning to understand the relationship between the numerator and denominator, but they may still view fractions as simply composites of the numerator and denominator rather than as numerical values with magnitude (Hamdan & Gunderson, 2017; Rinne, Ye, & Jordan, 2017). This underscores the significance of transitioning to the measurement representation of fractions. In this phase, students recognise fractions as distances from zero on a number line, reinforcing and deepening their understanding of magnitude. Their grasp of fraction density deepens as they see that the interval between zero and one can be partitioned into an infinite number of fractional values. This understanding leads to recognising that equivalent fractions represent the same magnitude and position on the number line, allowing for ordering and comparison (Hamdan & Gunderson, 2017).

As their understanding becomes more sophisticated, students begin to view fractions as ratios and rates, and eventually as operators. At these phases of the progression, they integrate foundational fraction concepts with their emerging multiplicative reasoning to further develop their symbolic proportional reasoning skills. Their knowledge of equivalent fractions helps them see how quantities in a ratio vary together. As students work with scaling ratios, they lay the groundwork for understanding multiplication of fractions and, ultimately, division of fractions.

Text box 2: Frameworks for fraction understanding

In the Mathematics Curriculum Frameworks (ACARA, 2024), initial fraction understanding is introduced in the Foundational Level as students “represent practical situations involving equal sharing and grouping with physical and virtual materials and use counting or subitising strategies” (AC9MFN06) and continue in Year 1 as students mathematically model these situations (AC9M1N06). In Year 2, students “recognize and describe one-half as one of 2 equal parts of a whole and connect halves, quarters and eighths through repeated halving” (AC9M2N03) by using part-whole models and fair-sharing activities. Measurement attributes of fractions are introduced as students “use and represent halves, quarters, and eighths in relation to shapes, objects and events” (AC9M2M02) and are applied to length, weight, and capacity. In Year 3, students use the part-whole model and fair-sharing to “recognize and represent unit fractions including ½, 1/3, ¼, 1/5 and 1/10 and their multiples in different ways and combine fractions with the same denominator to complete the whole” (AC9M3N02).

Students’ development of fraction understanding continues in Year 4 as they “find equivalent representations of fractions using related denominators and make connections between fractions and decimal notation” (AC9M4N03). Also in Year 4, students are expected to locate and represent fractions on number lines (AC9M4N04). Year 5 represents a shift to deeper applications of number lines such as interpreting, comparing and ordering rational numbers on number lines (AC9M5N01, AC9M5N03) and modeling addition and subtraction of fractions (AC9M5N05). Fraction concepts and procedures continue to develop in Years 5-8 with deeper understandings of equivalence and application of operations. In Years 7-8, students begin working with fractions as ratios as they “recognize, represent and solve problems involving ratios” (AC9M7N08) and rates as they “recognize and use rates to solve problems involving the comparison of 2 related quantities of different units of measure” (AC9M8M05). These skills set the foundation for future application of rational number concepts and skills in the remainder of secondary school.

Text box 3: Problems using equivalent fractions

When students begin to scale ratios, problems can be designed to support using their knowledge of equivalent fractions to solve for an unknown quantity, x, in proportions expressed symbolically. The sample problems below include how teachers can show students that the ratios covary in a proportion. Additionally, it is important to note that providing problems where the variable is in different positions supports students not over relying on moving from left to right when solving problems.

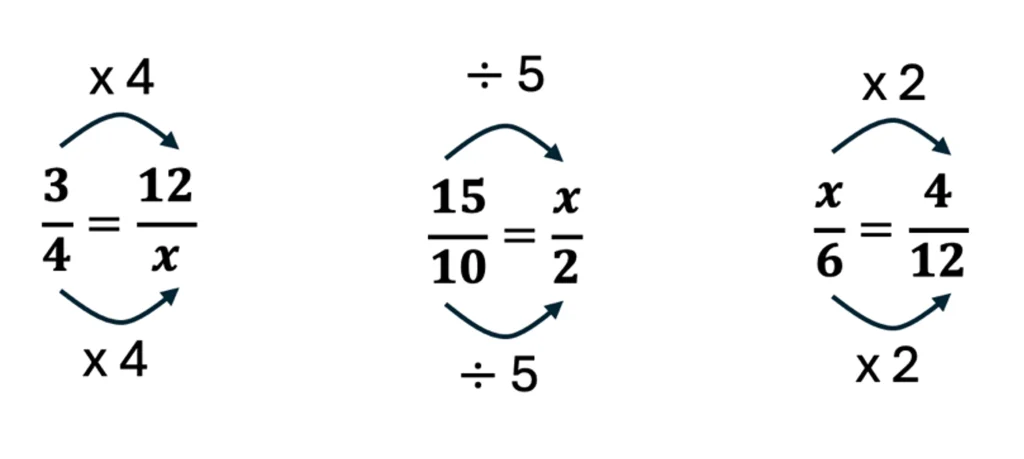
What does it look like in the classroom?

Using learning progressions in the classroom typically occurs during the planning phases of instruction. Planning should include consideration of how students develop fraction concepts and skills within the grade level, and how these skills will contribute to future learning in advanced grade levels. Because the learning progression for fractions spans multiple grades, it is important that teachers fully understand how students develop and use their fraction understanding to ensure continuity across grades.

1.1 Use learning progressions flexibly to identify a starting point and make connections by using models

The learning progression for fraction proficiency should not be viewed as static where instruction sequentially moves through phases or levels. Instead, it serves as a resource to guide teachers’ instructional decision-making, including when and how to use the instructional models as shown in Figure 2. For example, as teachers introduce new fraction concepts, they might connect these concepts to the area model to reinforce foundational part-whole fraction concepts before quickly advancing to more complex levels. Relatedly, as teachers collect data about students’ fraction understanding, they can associate that information to the learning progression. These insights help teachers determine students’ starting point, rate of instruction needed to help them reach their goals, and the possibility of persistent misconceptions in their understanding. The flexibility to navigate different phases of the learning progression and the use of various instructional models give teachers the adaptability needed for effective instruction.

Figure 2

Models for understanding fraction concepts

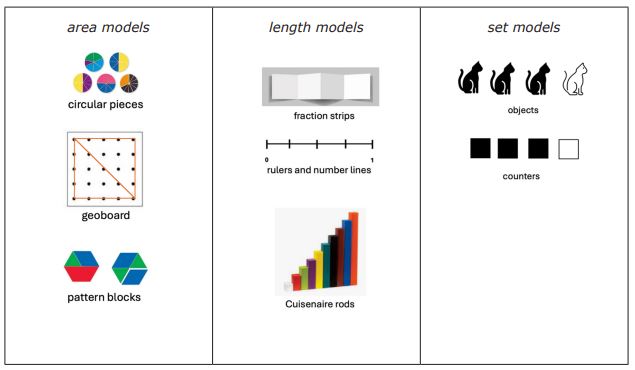
Figure 3

Learning progression for fraction understanding and associated examples (progressing in complexity from left to right)

1.2 Work progressively to build knowledge of fraction understanding

The learning progression of fraction concepts shown in Figure 3 spans multiple years of instruction.

Often, early instruction starts with the part-whole model, helping students formalise their emerging fraction concepts. Teachers can design activities that build students’ understanding of the relationship between the numerator and the denominator and support their comparison of fraction magnitude. Composing and decomposing fractions into units lays the foundation for operations with fractions (Braithwaite et al., 2021). A key learning outcome in these initial phases of learning is comparing fractions with different numerators but the same denominator. Instruction should intentionally integrate concrete representations (e.g., counters or pattern blocks) and semi-concrete representations (e.g., pictorial representations of the concrete models) while explicitly linking these experiences to formal fraction concepts, including fraction names (e.g., one-half) and fraction vocabulary (e.g., numerator). Figure 4 shows a micro-progression that develops students’ understanding of a unit and partitioning units for comparison.

Figure 4

A micro-progression for understanding a unit and partitioning units for comparison.

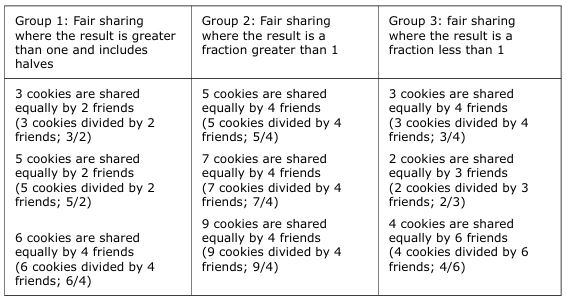
Instruction should then transition students to understanding fractions as fair-shares or quotients, connecting this with their prior informal exposure to early fraction concepts like sharing. Teachers can design activities where students share a set of objects or a single object equally among a group, emphasising the importance of creating equal-sized sets or parts. Increasing the size of the group among which the object(s) is shared reinforces the concept that partitioning a whole into more parts results in smaller shares. Wilson et al., (2011) designed a series of tasks that gradually increased the number of objects shared among an increasingly larger number of groups, extending students’ understanding. Figure 4 shows a carefully crafted progression of problems to support student understanding of fair sharing by first recognising that students are more familiar with halving and then progressing into other fractions greater than 1 and finally fractions less than 1.  Additionally, using concrete representations or manipulatives, such as counters or partitioned wholes like pizza, reinforces this concept. Explicitly linking these activities with abstract fraction notation helps students deepen their understanding. For example, when two friends share three cookies, the cookies are divided equally between the two. This can be represented as 3  2 or . Students may use different strategies to fair share (see Figure 5). Through this fair-sharing context, students begin to see the fraction bar as a representation of division.

Figure 5

Fair-sharing strategies when three cookies are shared equally by two friends

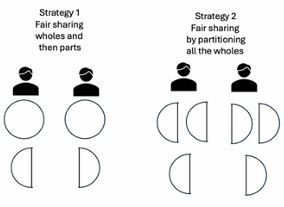
Figure 6

 Fair sharing problem progression

 Given the importance of the measurement model to students’ deep conceptual understanding of fractions, the number line is an essential instructional tool (Siegler et al, 2011) from which teachers can build on students’ knowledge of whole numbers to introduce and reinforce essential fraction concepts. When students model unit fractions end-to-end on a number line, the idea that fractions measure length becomes transparent, therefore reinforcing students’ conceptual understanding of magnitude (Braithwaite et al., 2021).

Interventions that integrate number lines into fraction instruction have significantly improved fraction outcomes for upper primary and lower secondary students with mathematics difficulty (Barbieri et al., 2020; Dyson et al., 2018; Fuchs et al., 2013). Bouck et al. (2023) offers a series of instructional activities incorporating number lines to teach fraction concepts for students with mathematics difficulty. Explicitly connecting fractions on the number line with previously introduced concrete representations (e.g., manipulatives) and semi-concrete representations helps students build on prior knowledge. Figure 7 in the next section gives a visual depiction of how this can work.

As students progress to lower secondary levels, understanding ratios and rates become a key instructional objective. Teachers can help students extend their fraction knowledge to think proportionally by connecting the part-whole and measurement models, both of which contribute foundational knowledge for proportional reasoning concepts like covariation. This knowledge lays the groundwork for operations with fractions, where students apply proportional reasoning to view multiplication as scaling an original value (either up or down) based on the ratio. To make sense of fraction operations, teachers can use semi-concrete representations like area models or number lines to illustrate the outcomes of fraction operations.

Text Box 4: Scaling 3 up by multiplying it by 3/2

A number line can be used to link to students’ existing understandings of operations with whole numbers and give meaning to operations with fractions.

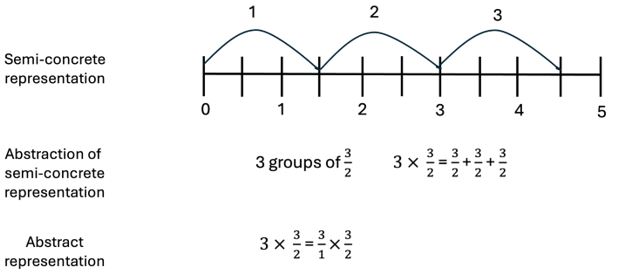
(Adapted from Fuchs et. al., 2021)

1.3 Ensure students have mastered previous understandings of fractions

It is important to note that some students may have varying levels of prior knowledge as it relates to fraction concepts and skills. Students’ prior knowledge should be identified before beginning instruction on fraction concepts and skills. By identifying where along the learning progression students have demonstrated mastery, teachers can reinforce those concepts and skills before moving into new learning. For example, if the instructional unit focuses on adding fractions with unlike denominators but some students have not fully grasped a measurement understanding of fractions, these students may struggle to learn the new concepts. Teachers can use the learning progression to provide individualised instructional support, as needed.

Relevant teacher resources for Practice 1:

1. Bouck, E., Bouck, M., & Anderson, R. D. (2023). Teaching fractions to elementary students with learning disabilities using evidence-based practices. Intervention in School and Clinic, 1-6.
2. Siemon, D. (2003). Partitioning: The missing link in building fraction knowledge and confidence. The Australian Association of Mathematics Teachers, 59(3), 22-24.
3. Fraction circles, fraction tiles, and number lines manipulatives https://www.didax.com/searchresults.html?menu=math&subject=95&topic=77
4. Geoboard, counters, and pattern blocks virtual manipulatives https://www.didax.com/virtual-manipulatives.html
5. Intervention lessons on equivalent fractions, ratios/rates, and proportionality https://meadowscenter.org/resource/mstar-interventions/

Practice 2: Build coherence across number systems, focusing on magnitude

What is this practice?

As students move from their early, informal experiences with quantities to more formal mathematics concepts, they learn key ideas, such as how symbolic numbers represent quantities, how numbers are sequenced based on their magnitude, and how these sequences can be used to order and compare numbers. These concepts highlight the significance of understanding magnitude, which is a key principle behind all real numbers. A solid grasp of whole number magnitude gives students the foundation they need to understand fractions concepts and procedures (Bailey, Siegler, & Geary, 2014; Rinne, Ye, & Jordan, 2017; Siegler, 2016). This emphasises the need to design instruction that builds on students’ understanding across number systems in a coherent and connected manner.

Teaching fractions in a way that builds on students’ whole number knowledge, explicitly linking commonalities while calling out key differences, helps students make connections between prior knowledge and new concepts. Additionally, intentional integration of concepts can prevent common challenges, such as the misapplication of whole number concepts and procedures when learning fractions.

What is the research?

Building an understanding of fraction magnitude begins with understanding whole number concepts. Siegler (2016) synthesised research showing that the progression from non-symbolic to symbolic representations of whole numbers magnitude lays the groundwork for understanding fraction magnitude, as well as the magnitude of decimals and negative numbers. Longitudinal studies support this, showing that students who have a strong grasp of whole number magnitude in first grade are better equipped to learn fraction magnitude, which then facilitates their understanding of fraction arithmetic by early secondary (Bailey et al., 2014). A key aspect of this progression is the development of a mental number line, which helps students accurately represent fraction magnitudes, as seen when they locate fractions on a number line (Mou et al., 2016).

However, students’ understanding of whole numbers can sometimes interfere with learning fraction concepts. Students often mistakenly treat the numerator and denominator as separate whole numbers, leading them to apply whole number rules when evaluating fraction magnitude. This misconception, known as the ‘natural number bias’ (Braithwaite et al., 2021; Meert, Gregoire, & Noel, 2010; Van Hoof, Verschaffel, & Dooren, 2015), can be detected when students compare fractions. For example, they might incorrectly assume that the fraction with the larger numerator is greater, without considering the denominators. As students begin to understand the role of the denominator, they may then overcorrect and rely solely on the denominator to compare fractions. It is only when students fully comprehend the relationship between the numerator and the denominator that they can accurately compare fractions (Mou et al., 2016; Rinne et al., 2017). The natural number bias is discussed in more depth in Practice 4.

What does this look like in the classroom?

2.1 Use the number line as a tool to teach fraction magnitude

Given the importance of understanding fraction magnitude, it is essential for teachers to focus instruction on this concept. Rinne et al., (2017) cautioned that students who do not develop a solid foundation in fraction magnitude by the end of Grade 5 may persistently struggle with both conceptual and procedural aspects of fractions. Therefore, it is crucial that students build a strong sense of fraction magnitude concepts in primary school. Teachers can support this understanding by connecting students’ knowledge of whole number magnitude to their emerging understanding of fraction magnitude (Ketterlin-Geller & Chard, 2011). A key tool for this is the number line, which helps students visualise and grasp fraction concepts.

2.2 Deliberately build on whole number magnitude knowledge

Teachers can help students understand fraction magnitude by building on their whole number knowledge. This begins with ensuring that students have a solid grasp of whole number magnitude. Teachers can then explicitly connect whole number concepts to fraction concepts, highlighting both similarities and differences across number systems (Bailey et al., 2014; Rinne et al., 2017). A fundamental similarity is that all real numbers have magnitude and can be placed on a number line. Building on students’ experience with equal interval spacing of whole numbers on a number line, teachers can help students understand that the interval between whole numbers can be partitioned into fractions (Rinne et al., 2017). Zhang et al. (2017) noted that students with mathematics difficulties may need explicit instruction on using a number line to represent fractions, emphasising the definition of a unit.

As shown in Figure 7, teachers can superimpose fraction strips on a number line to emphasise the connection between part-whole, quotient, and measurement representations of fractions. Students can practise locating fractions as well as using the number line to compare the magnitude of two fractions. This reinforces the idea that fractions are measures of quantity. As students deepen their understanding of fractions on the number line, other concepts such as fraction density and equivalence can be introduced.

Figure 7

An example of a teacher explaining how a number line can be superimposed with fraction strips to show how one whole and four fourths are equivalent.

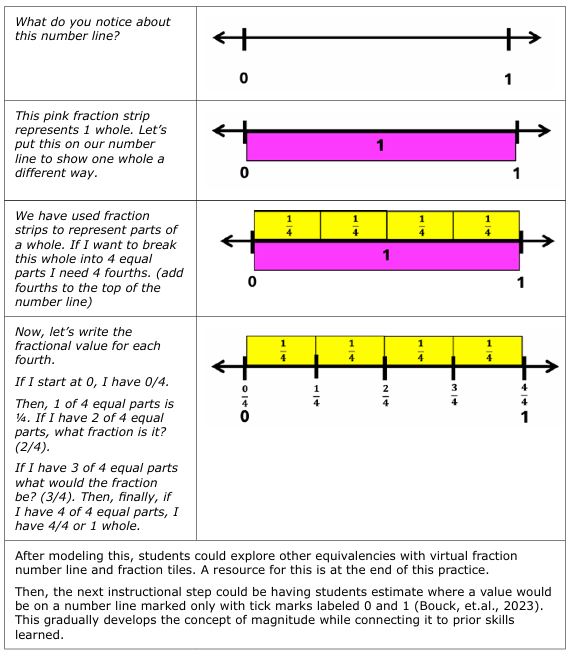
Note: This can be used to build the connection between part-whole and measurement models of fractions by focusing on the ‘distance’ rather than the parts of the whole.

2.3 Help students develop fluency in accessing knowledge about fraction magnitude

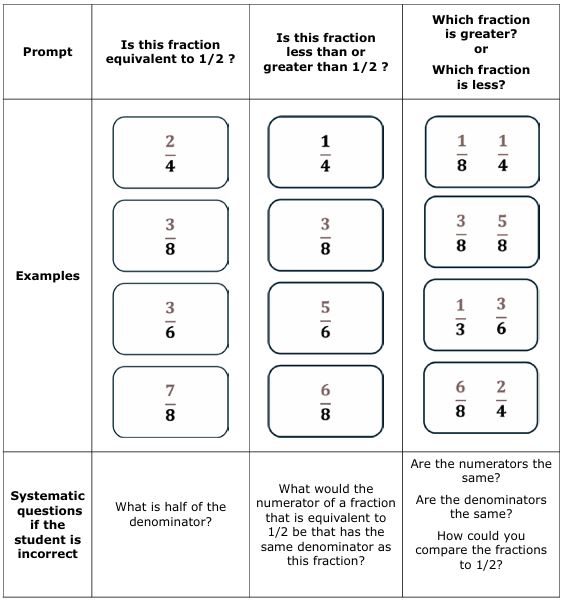
To help students internalise fraction magnitude concepts, Fuchs et al. (2017) recommend incorporating brief fluency-building activities into instruction. These can be quick, one-minute exercises that promote automaticity with fraction magnitude. It is important to use fluency-building activities after students have had an opportunity to learn and practise an efficient strategy for solving these types of problems. In Figure 8 below, three examples of one-minute fluency-building activities are shown. For each example, the teacher explains to the students that each time they see a fraction on the card they will answer the prompt. For the first one, the teacher would show a fraction and ask, “is this fraction equivalent to ½?” The student would respond with “yes” or “no”. If correct, the teacher moves to the next card. If incorrect, the teacher can ask systematic corrective questions to support the student in getting the correct answer. After the student corrects their answer, the card goes in the completed pile. The goal is to get more problems correct each day during the one-minute activity.  For students with low working memory capacity, allowing them to explain their reasoning after these exercises was shown to improve their fraction magnitude performance.

Figure 8

Quick one-minute fluency flashcard activities.

Text box 5: Importance of fluency

Automatic fact retrieval is a core component of mathematics intervention (Fuchs et al., 2021). When students have automaticity with the basic facts or steps of a mathematics problem, they have greater cognitive capacity to think through the more challenging tasks or multiple steps of the problem (Fuchs et al., 2021). Additionally, students’ fluency with addition (Hecht & Vagi, 2010; Jordan et al., 2013), fluency with multiplication (Hansen et al., 2015; Hecht & Vagi, 2010), and skill with long division (Hansen et al., 2015) are each essential in the development of students’ fraction knowledge.

Teachers can promote their students’ automaticity with these whole number arithmetic facts, as well as subtasks of fraction problems, by incorporating timed activities as one piece of their mathematics instruction (Fuchs et al., 2021). With timed activities, teachers should evaluate how facts (e.g., whole number arithmetic) and subtasks (e.g., naming equivalent fractions of the ½ benchmark fraction) could support students in their understanding of fraction concepts and procedures.

Teachers can minimise student anxiety in timed activities by ensuring their students are aware that they don’t need to solve all problems on a worksheet (Fuchs et al., 2021). Teachers can also rely on flashcards to show fewer problems at a time or group activities to encourage collective performance. Students should be encouraged to focus on individual progress through scoring “personal bests” rather than being compared with other students.

2.4 Use diagnostic tasks to identify misconceptions based on whole number understandings

Teachers can design tasks to identify whether students’ whole number knowledge is interfering with their understanding of fraction magnitude. Comparison tasks can be effective in detecting natural number bias (Mou et al., 2016; Rinne et al., 2017). However, it is important to carefully construct these tasks to focus on specific comparisons. For example, asking students to compare 4/9 and 2/7 may not reveal much about their potential natural number bias, because the magnitudes of both numerators and denominators align with whole number reasoning. For a more accurate assessment, tasks should involve fractions where either the numerators or denominators (or both) do not follow whole number logic. For instance, comparing 3/7 and 4/5 can show if students are focusing solely on numerators. If they incorrectly selected 3/7, it could indicate that they are influenced by whole number thinking. Presenting fractions like ¾ and 5/9, where both numerators and denominators are incongruent with whole number magnitude comparisons, can better reveal students’ depth of understanding.

Although whole numbers and rational numbers share properties of all real numbers, whole numbers also have unique characteristics that do not generalise to other number systems. It is important to highlight these three distinctions:

1. Whole numbers have a unique predecessor and successor, as seen in counting sequences. Fractions and decimals do not have unique successors because there are infinitely many fractions between any two points on a number line, (e.g., fraction density). Teachers can help dispel the belief that there are no numbers between 1-2 or between 2/5 and 3/5 through intentionally designed activities, such as zooming in on portions of a number line, as shown in Figure 9. Moreover, during early instruction on whole number concepts, teachers should avoid definitive statements that are only true with whole numbers such as “there is always one number that comes before and after any other number”.
2. Whole numbers are represented by unique symbols, while fractions can be expressed in countless equivalent forms that represent the same quantity. Teachers can emphasise the equivalence with semi-concrete representations such as fraction strips.
3. Whole number operations follow consistent patterns (e.g., addition and multiplication always increase or maintain a whole number’s value, while subtraction and division decrease or maintain it) that do not hold true for fractions. Teachers should avoid definitive statements such as “multiplying always makes a bigger number” or “dividing always makes a smaller number” because these do not hold true for fraction multiplication and division. The oversimplified rules can lead to confusion as students encounter more complex concepts and expand the number systems.

Figure 9

 Modeling using a magnifying glass to Zoom into a portion of a number line.

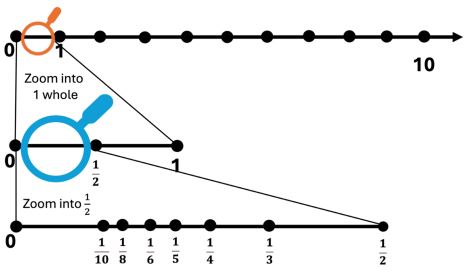
Teachers should be mindful of these distinctions and teach for transfer across number systems. Teachers should explicitly explain that some properties apply only to whole numbers and not to other number systems. Karen Karp and colleagues (2014) compiled a helpful list of 13 ‘rules’ that expire from early primary through to early secondary. Avoiding introducing concepts and cementing rules that will eventually expire is important. Early grade teachers are encouraged to bring coherence across the number systems by understanding the impact of teaching non-conceptually based ‘tricks.’

Relevant teacher resources for Practice 2:

1. Karp, K. S., Bush, S. B., & Dougherty, B. J. (2014). 13 rules that expire. Teaching Children Mathematics, 21(1), 18-25.
2. Fraction tiles and fraction number line virtual manipulative https://www.didax.com/apps/fraction-number-line/
3. Online games for fluency practice
   1. https://www.ixl.com/math
   2. https://home.xtramath.org/
4. Dice and spinner virtual manipulatives for fluency practice
   1. https://toytheater.com/dice/
   2. https://www.didax.com/apps/spinners/

Practice 3: Systematically and intentionally link fraction concepts with procedures

 What is the practice?

It has long been argued that conceptual understanding and procedural fluency must coexist for students to truly grasp mathematics (Ball et al., 2005). These elements, intertwined with students’ ability to reason quantitatively, apply strategies, and think mathematically, form the foundation of mathematical proficiency and problem-solving (National Academies of Sciences, Engineering, and Medicine [NASEM], 2001). Because of the complexity (and the difficulty experienced by many students) of learning fractions, students’ ability to integrate fraction concepts and procedures is never more important.

Students with conceptual understanding can see relations across concepts, understand the meaning of operations, evaluate the reasonableness of solutions, and can mathematically justify their responses.

Procedural fluency is defined as knowing procedures, when and how to use them appropriately, and performing them flexibly, accurately, and efficiently (NASEM, 2001). It is not just about performing operations quickly but about solving problems efficiently, identifying and correcting errors, applying algorithms in contextualised settings, and generalising understanding to novel situations. Procedural fluency allows students to devote more of their attention to solving complex problems, connecting procedures with concepts, and seeing relationships between quantities.

When teaching fractions, conceptual understanding and procedural fluency should be systematically integrated. Students should connect and differentiate whole number concepts with fraction concepts, link fraction concepts to fraction arithmetic, and understand the similarities and differences between whole number and fraction arithmetic (Ketterlin-Geller et al., 2019). By recognising these complex interactions, students can build a strong, coherent understanding of fraction concepts and the rules that govern fraction operations.

What is the research?

In their review of fraction intervention research, Roesslein and Codding (2019) identified only a few studies that explored the connection between conceptual and procedural knowledge for primary students. However, experimental studies in cognitive psychology highlight the important relationship between conceptual understanding and procedural fluency for both whole numbers and fractions.

Because whole number arithmetic skills are essential for fraction computation, students must first be proficient with whole number operations before successfully executing fraction operations. Inaccuracies with whole number calculations will impact fraction calculations. That said, whole number and fraction arithmetic procedures only partially overlap. So, to develop procedural fluency with fraction arithmetic, students need to understand the meaning underlying the operations (Siegler & Lortie-Forgues, 2017). To make sense of the operations, students need to understand how arithmetic operations transform magnitudes when applied to both whole numbers and fractions (Lortie-Forgues, Tian, & Siegler, 2015).

A longitudinal study by Bailey and colleagues (2014) found that the connection between early understanding of whole number magnitude and later success with fraction arithmetic was fully mediated by students’ understanding of fraction magnitude. This shows that while proficiency in whole number concepts and procedures is necessary for fraction computations, students must also develop a strong conceptual grasp of fractions.

Specifically, understanding fraction magnitude is a key precursor to successful fraction computation (Siegler & Lortie-Forgues, 2017). When students misunderstand fraction magnitude, they are more likely to have difficulties with fraction arithmetic, including both implementing the procedures and evaluating the reasonableness of their answers (Braithwaite et al., 2021). In an experimental study, Jordan and colleagues (2013) found that students’ understanding of fraction magnitude was the strongest predictor of their fraction arithmetic skills, although other factors like working memory, attentiveness, and calculation fluency also played significant roles. Similarly, Fuchs et al., (2013) demonstrated that explicit instruction in fraction magnitude concepts led to significant improvements in students’ fraction arithmetic skills. These findings emphasise the importance of building students’ understanding of fraction concepts to support their ability to apply fraction procedures effectively.

What does it look like in the classroom?

Instruction of fraction concepts and arithmetic spans multiple grades, so it is important for teachers to collaborate in developing coherent approaches that build students’ knowledge across grades. Teachers in earlier grades have a unique responsibility to design instruction that helps students transport and integrate their understanding of both whole numbers and fractions, including both conceptual understanding and procedural fluency.

3.1 Establish the need for fractions early through activities involving whole numbers

First, early learning of whole number concepts and procedures should be designed to facilitate the introduction of fraction concepts and procedures by supporting students in seeing the need for fractions. Teachers can consider natural extensions that help students see their value. For example, students can participate in class activities like mini-Olympics that require measurement. Through activities like the standing long jump, students can discover the need for more accurate measurements, which could lead to the need for fractional values (Barnett-Clarke et al., 2010).

3.2 Use representations that work for both whole numbers and fractions

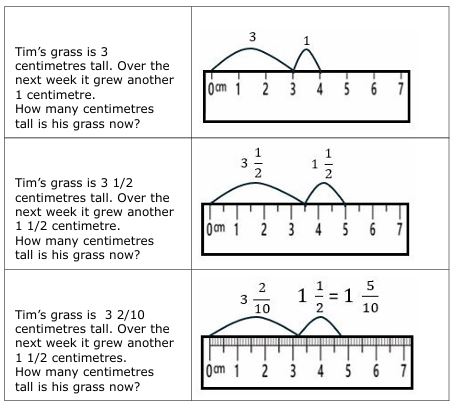
Teachers can also support this transition by systematically using targeted concrete and semi-concrete representations. For example, teaching whole number concepts on a number line sets the stage for introducing fraction concepts (Bailey et al., 2014). Additionally, semi-concrete representations like area models and number lines can be used to teach whole number arithmetic in a way that builds on students’ understanding of magnitude. Using a ruler to support fraction addition and subtraction, as shown in Figure 10, help students make these connections (Van de Walle et al., 2016). Starting with whole number rulers and then gradually transitioning to rulers that show parts of wholes (e.g., half centimetres and then millimetres) can support students understanding of magnitude.

Because many students have difficulty conceptually understanding fraction operations, using these same instructional models when teaching fraction arithmetic can support transfer of students’ whole number knowledge as well as emphasise the underlying meaning of the operations. For students who struggle with fractions, instruction that systematically incorporates concrete representations or manipulatives and semi-concrete representations improves their conceptual understanding and arithmetic skills as compared to typical instruction.

Figure 10

Application of rulers with different tick marks to support developing addition and subtraction as magnitude.

3.3 Teach whole number operations in a way that generalises to fraction arithmetic

Early whole number arithmetic instruction should be taught in a way that it can serve as an anchor for instruction on fraction arithmetic. Teachers need to ensure that students develop a solid conceptual foundation in whole number arithmetic using language that is transferable (Lortie-Forgues et al., 2015). For example, teaching multiplication of whole numbers only as repeated addition may not transfer well to fractions. Instead, teaching multiplication m x n as ‘m of the ns’ (e.g., 5 x 3 is the same as 5 of the 3s) can smoothly transition to fraction multiplication (e.g., 2/5 x 1/3 is the same as 2/5 of the 1/3). Similarly, teaching whole number division as ‘fair sharing’ may not fully support understanding fraction division. Instead, explaining both as “how many times the divisor can go into the dividend” (e.g., how many times 5 goes into 45; how many times ¾ goes into ½) provides a consistent approach across both whole numbers and fractions.

When it comes to addition and subtraction of fractions, similarities with whole number operations should be highlighted (e.g., combining or separating units), but key differences must also be emphasised. For instance, presenting individual fractions and their sums or differences as composites of unit fractions can help students understand these operations (Braithwaite et al., 2021) and build connections to the properties of operations, as shown in this example: 1 ¼ + ¾ = (1 + ¼) + (¼ + ¼ + ¼) = (1 + (¼ + ¼ + ¼ + ¼) = 1 + 1 = 2. Additionally, teachers can use a progression to support solving problems with unlike denominators as shown in Figure 11. These problems are best designed in context and using semi-concrete representations. When having a class discussion, teachers can focus on creating an equivalent problem with equal-sized parts.

Figure 11

Progression of unlike denominator problems

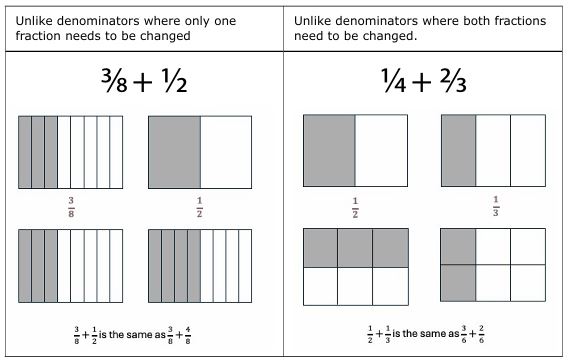
Teachers should also emphasise the role of the denominator in defining the number of parts, which is crucial for understanding the need for a common denominator when adding or subtracting fractions. This also helps clarify why denominators are not added or subtracted in the algorithm, thereby connecting students’ conceptual understanding with their procedural skills.

3.4 Plan for students to articulate thinking during problem solving

Instructional activities should be designed to encourage students to articulate their conceptual and procedural understanding while solving problems. Braithwaite et al., (2019) noted that students use various strategies — both effective and not effective — when tackling fraction arithmetic problems. A helpful instructional approach is to have students explicitly state the arithmetic strategy they plan to use before solving the problem — allowing them to articulate their reasoning based on the problem’s relevant features. To further support sense-making, students can estimate the outcome and evaluate the plausibility of their estimate, using activities like the one shown in Figure 11. If their estimate is implausible, it can signal errors in their reasoning or incorrect application of procedures (Braithwaite et al., 2021), encouraging students to reflect on their own understanding. By verbalising their intentions, students can better connect fraction concepts and procedures, and teachers can provide corrective feedback.

For students who struggle, teachers can model explanations and support students’ generation of valid explanations with the same positive effects on student outcomes (Fuchs et al., 2017). Activities like the one shown in Figure 7 in Practice 2 and Figure 12 below, can be used to support fluency with fractions, as classroom routines that take up to 10 minutes, rather than the focus of an entire lesson. Teachers may find it helpful to use the same classroom routine focus for 5-10 days and then transition to a different focus for the routine to support student growth over time within and across skills. Classroom routines focused on fluency encourage students to share their strategies, reflect on the strategies of others, and support the development of more efficient strategies. While it is more common to use classroom fluency routines to develop skills with whole numbers, these routines can also be successfully applied with fractions.

Figure 12

Thumbs up or Thumbs Down Estimation

Note: adapted from Van de Walle et al., 2016.

 Relevant teacher resources for Practice 3:

1. Barnett-Clark, C., Fisher, W., Marks, R., & Ross, S. (2010). Developing essential understanding of rational numbers for teaching mathematics in grades 3-5. National Council of Teachers of Mathematics.
2. Woodward, J., Beckmann, S., Driscoll, M., Franke, M., Herzig, P., Jitendra, A., Koedinger, K. R., & Ogbuehi, P. (2012). Improving mathematical problem solving in grades 4 through 8: A practice guide (NCEE 2012-4055). Washington, DC: National Center for Education Evaluation and Regional Assistance, Institute of Education Sciences, U.S. Department of Education. Retrieved from http://ies.ed.gov/ncee/wwc/publications_reviews.aspx#pubsearch/.
3. Examples of classroom videos focused on fluency routines with whole numbers: https://www.insidemathematics.org/classroom-videos/number-talks

Practice 4: Systematically and immediately address misconceptions and errors

What is this practice?

Errors and misconceptions can be harmful to a student’s current and future mathematics learning. If they are not remediated, mathematics errors can be systematic and continuous throughout a student’s mathematics education (Hwang & Riccomini, 2021). Yet, teachers can use their students’ errors and misconceptions as powerful tools for guiding instruction, as teachers can gain individualised, in-depth diagnostic information about their students’ conceptual or procedural gaps. With this information, teachers can provide more targeted mathematics instruction and intensification that systematically addresses the errors and misconceptions before they become persistent.

To analyse students’ fraction errors and misconceptions, teachers can synthesise fraction errors into four categories:

1. errors associated with natural number bias
2. misapplications of fraction operations, procedures or algorithms
3. errors with whole number arithmetic in fraction problems, and
4. errors on word problems involving fractions (Powell & Nelson, 2021).

What is the research?

Natural number bias

Natural number bias is characterised as a student’s misapplication of the concept of counting natural or whole numbers as single units when interpreting fractions, leading them to have trouble with viewing a natural or whole number as a unit that is decomposable (Ni & Zhou, 2005).

While there are differing explanations of how the natural number bias originates (e.g., innate vs. learned), research indicates that instruction favouring discrete numbers over continuous numbers plays a role in generating students’ natural number bias (Ni & Zhou, 2005). However, students’ numerical development can be unified by the progression of their magnitude understanding across non-symbolic whole numbers, symbolic whole numbers, large whole numbers, and rational numbers (Siegler & Lortie-Forgues, 2014).

Natural number bias can be associated with a student’s misconceptions or errors with fraction concepts (e.g., congruence, magnitude, equivalence) (Ni & Zhou, 2005). Natural number bias may be at work in a student’s reasoning about fractions when a student believes that there are no numbers between 0 and 1. Also, a student might confuse the concepts of the size of a partition’s elements and the number of elements, such as reasoning that ⅙ must be greater than ½ since 6 is greater than 2.

Natural number bias may also be present when operating with fractions. In their analysis of 9^th and 10^th grade algebra students’ errors on fraction problems, Brown and Quinn (2006) found that students demonstrated the error of adding or subtracting numerators and denominators across for problems involving fraction addition and subtraction — extending the concept of whole number addition and subtraction to fraction operations. When asked whether the quotient from dividing two fractions was less than or greater than ½, almost half of the students answered incorrectly, likely transferring their whole number division reasoning that the quotient should be less than the dividend to their thinking about fraction division.

Misapplications of fraction concepts, procedures or algorithms

A likely consequence of students learning algorithms for fraction operations without a foundational basis of the concepts is perpetual errors and misconceptions. Newton et al. (2014) identified error patterns made by sixth graders with learning disabilities on computational problems with simple fractions, mixed numbers, and whole numbers that illustrate the misapplication of fraction concepts and procedures. Some examples of common misconceptions are shown in the table below.

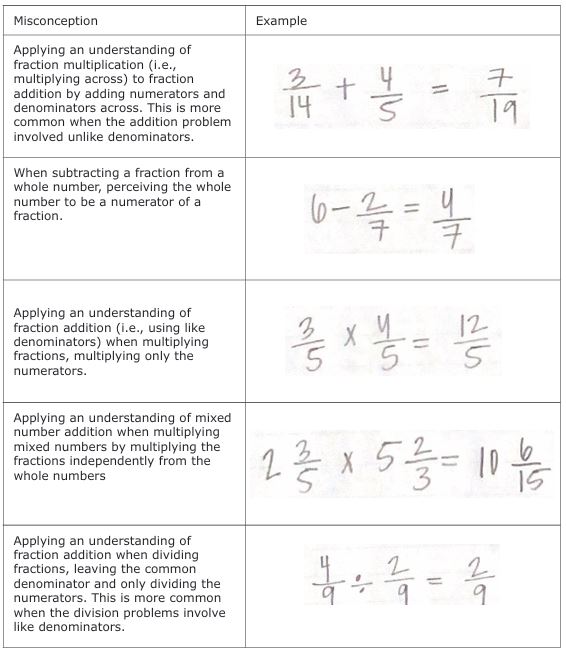
Students can also develop the misconception that the algorithm appropriate for the fraction operation depends on whether the fractions have equal denominators. Newton et al. (2014) showed that students were prone to add numerators and denominators across on fraction addition problems with unlike denominators. Students were prone to incorrectly keep the common denominator on fraction multiplication and division problems with like denominators.

 Errors with whole number arithmetic in fraction problems

Students’ difficulty with whole number operations and calculations can show up as errors in their solutions to fraction operations (Powell & Nelson, 2021; Lortie-Forgues et al., 2015). Lortie-Forgues et al. (2015) argue that fraction arithmetic necessitates students to have proficiency with whole number operations, as whole number arithmetic is interrelated with fraction procedures like converting between mixed numbers and fractions, finding fractions that are equivalent, and simplifying fractions. Newton et al., (2014) found that the most frequent skill error made by 6^th graders with learning disabilities in their study was errors with converting between mixed numbers and fractions, which they suggested derived from weak arithmetic fluency.

 Errors on word problems involving fractions

Powell and Nelson (2021) found in their rational number error analysis that the error patterns made on word problems involving rational numbers included misapplying procedures and natural number miscalculations. Brown and Quinn (2006) demonstrated that on word problems with fractions, students exhibited difficulty with identifying the appropriate operation to use and used algorithms that were disjointed with numbers in the word problem.

What does it look like in the classroom?

Natural number bias

4.1 Use number lines, comparing and ordering tasks to support a measurement understanding of fractions

Teachers can promote their students’ progression of whole number magnitude understanding to fraction magnitude understanding by showing students that they can represent the magnitudes of both whole numbers and fractions on a number line (Siegler & Lortie-Forgues, 2014). Educators should also explicitly teach the whole number properties that do not carry over to fractions (e.g., a single symbol represents a whole number; there is a unique successor for whole numbers).

Teachers should use the number line representation to develop their students’ understanding of fraction magnitude. Schumacher and Malone (2017) showed that instruction targeting students’ understanding of fraction magnitude reduced 4^th grade students’ application of errors demonstrating natural number bias when adding and subtracting fractions. The magnitude-focused instruction from their study began with connecting students’ part-whole understanding of fractions to the measurement model, then targeted students’ fraction magnitude understanding through activities involving comparing two fractions, ordering three fractions, and putting fractions on number lines. Students also considered how the magnitude of a fraction related to 0, ½, and 1.

When comparing fractions, focusing on a sequence of problems that support students in transitioning from a part-whole model to a measurement model can be helpful, especially if the teacher focuses on number lines in whole group discussions (Freeman & Jorgensen, 2015). Using a sequence of problems would need to occur over time, not all at once or within one day. A sequence of problems is shown in Figure 13.

Figure 13

Example of sequence of comparison problems

4.2 Use pictorial representations to support fraction division

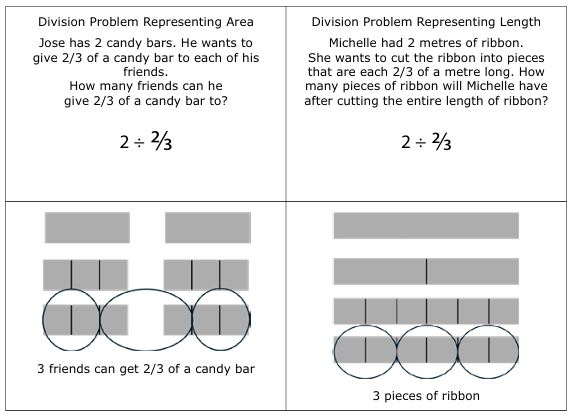
To address fraction division errors associated with natural number bias, teachers should give students opportunities to interpret word problems by pictorially representing fraction division (Brown & Quinn, 2006). Figure 14 below shows examples that represent the division of whole numbers by proper fractions to demonstrate that the quotient may not always be less than the dividend in division.

Figure 14

 Examples of fraction division word problems

Misapplications of fraction concepts, algorithms or procedures

4.3 Develop students’ understanding of the conceptual basis for procedures and algorithms

To combat students’ errors associated with the misapplication of fraction operation algorithms, teachers should ensure students have a strong understanding of the underlying concept of the operation before exposure to the algorithm (Brown & Quinn, 2006). Without conceptual understanding, students may give unreasonable solutions, misapply algorithms, or apply inappropriate algorithms (Powell & Nelson, 2021).

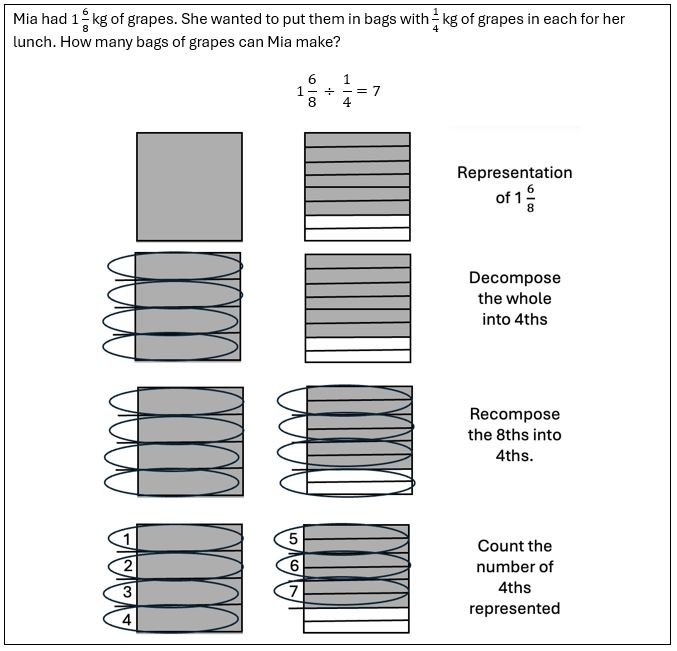
For instance, when introducing students to fraction division, teachers can support their students’ learning by incorporating measurement division story problem-solving, in which students develop a common-denominator algorithm for dividing fractions through relying on their pictures (Cramer et al., 2010) as shown in Figure 15.

Figure 15

Example of measurement division story problem

Teachers can also incorporate both concrete representations (e.g., pattern blocks, fraction circles, two-sided counters, Cuisenaire rods, fraction bars, square tiles, connecting cubes, fraction tiles) and semi-concrete representations (e.g., strip diagrams, tables, line plots, bar graphs, number lines) to teach fraction concepts and operations (Fuchs et al., 2021). Teachers should systematically integrate multiple representations during instruction and emphasise the alignment between them. It is important to associate symbolic notation across representations.

Finally, teachers can help students differentiate when to keep or find the common denominator during fraction arithmetic (i.e., addition, subtraction) compared to when to apply the operation to both the numerator and denominator (i.e., multiplication, division) (Lortie-Forgues et al., 2015). Teachers can highlight the differences in the procedures for solving fraction addition and multiplication problems that involve the same fractions, as well as emphasise the consistent use of the procedure for fraction division regardless of whether the fractions have unlike or like denominators (Newton et al., 2014).

Errors with whole number arithmetic in fraction problems

4.4 Support students to develop fluency with whole number operations

Teachers should incorporate fact fluency practice with whole numbers to help prevent whole number miscalculation errors during fraction operations. Teachers can use timed activities (i.e., 1-5 minutes) to develop their students’ automatic retrieval of whole number operation facts, enhancing problem difficulty as students’ fluency increases and incorporating mixed practice with the operations (Fuchs et al., 2021). For example, teachers can target students’ fluency with whole number multiplication facts during timed activities to assist students with finding common denominators when adding and subtracting fractions.

When developing fluency with multiplication facts, it is valuable to start with facts students know. In Figure 16, teachers can individualise flash cards by helping students identify a related fact that can be used as a starting place. For example, if a student does not have automaticity with 4 x 8, but 2 x 8 is a familiar fact, they could start with 2 x 8 and double it.

Alternatively, if a student does not have automaticity with 6 x 7 but knows 5 x 7 is 35, they can add 7 more to get 42, the answer to 6 x 7. Another student might choose to start with 2 x 7 = 14 and then add 14 + 14, which represents 2 x 7 + 2 x 7 + 2 x 7 = 6 x 7. By utilising x 2 and x5 facts, students can gain more automaticity over time.

Figure 16

Example of flash cards with a related fact

Errors on word problems involving fractions

4.5 Explicitly teach students to solve different types of word problems involving fractions.

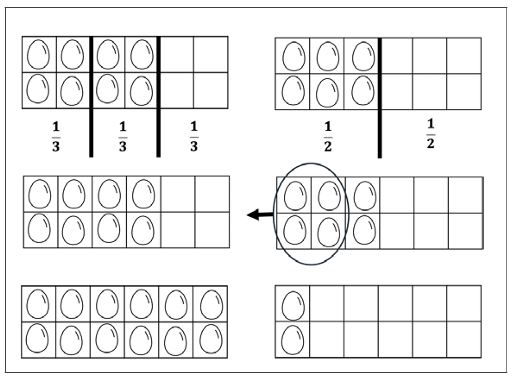
Finally, teachers should implement explicit instruction on rational number word problems with a range of problem types, including problems addressing sets, non-circular areas, and length (Powell & Nelson, 2021). Teachers can represent sets in their word problems like the one shown in Figure 17 by “eggs in cartons”, non-circular areas as “a rectangular backyard” and length as “growth of plants” (p. 325). Teachers can develop their students’ knowledge of appropriate strategies for solving a word problem based on its meaning, as well as use think-alouds to introduce an attack strategy to effectively support their students in word problem solving (Powell & Fuchs, 2018).

Figure 17

Example of word problem with a set model

On Monday, Evelyn gathered  of a carton of eggs. On Tuesday, she gathered  of a carton of eggs. If each carton holds a total of 12 eggs, how many eggs does Evelyn have now?

Relevant teacher resources for Practice 4:

1. Cramer, K., Monson, D., Whitney, S., Leavitt, S., & Wyberg, T. (2010). Dividing fractions and problem solving: Reflect and discuss.Mathematics Teaching in the Middle School, 15(6), 338–346. http://www.jstor.org/stable/41183034
2. Fuchs, L.S., Newman-Gonchar, R., Schumacher, R., Dougherty, B., Bucka, N., Karp, K.S., Woodward, J., Clarke, B., Jordan, N. C., Gersten, R., Jayanthi, M., Keating, B., and Morgan, S. (2021). Assisting Students Struggling with Mathematics: Intervention in the Elementary Grades (WWC 2021006). Washington, DC: National Center for Education Evaluation and Regional Assistance (NCEE), Institute of Education Sciences, U.S. Department of Education. Retrieved from http://whatworks.ed.gov/.
3. Siegler, R., Carpenter, T., Fennell, F., Geary, D., Lewis, J., Okamoto, Y., Thompson, L., & Wray, J. (2010). Developing effective fractions instruction for kindergarten through 8th grade: A practice guide (NCEE #2010-4039). Washington, DC: National Center for Education Evaluation and Regional Assistance, Institute of Education Sciences, U.S. Department of Education. Retrieved from whatworks.ed.gov/ publications/practice guides.

References

Practice 1

Australian Curriculum, Assessment and Reporting Authority [ACARA]. (2024). Australian Curriculum: Mathematics F-10 Version 9.0. https://v9.australiancurriculum.edu.au/downloads/learning-areas#accordion-b71b085f07-item-f1428171c5

Barbieri, C. A., Rodrigues, J., Dyson, N., & Jordan, N. C. (2020). Improving fraction understanding in sixth graders with mathematics difficulties: Effects of a number line approach combined with cognitive learning strategies. Journal of Educational Psychology, 112(3), 628-648.

Bouck, E., Bouck, M., & Anderson, R. D. (2023). Teaching fractions to elementary students with learning disabilities using evidence-based practices. Intervention in School and Clinic, 1-6.

Braithwaite, D. W. & Siegler, R. S. (2021). Putting fractions together. Journal of Educational Psychology, 113(3), 556-571.

Confrey, J. (2018). Future of Education and Skills 2030: Curriculum Analysis – A Synthesis of Research on Learning Trajectories/Progressions in Mathematics (EDU/EDPC[2018]44/ANN3). Organisation for Economic Co-operation and Development.

Dyson, N. I., Jordan, N. C., Rodriguez, J., Barbieri, C., & Rinne, L. (2018). A fraction sense intervention for sixth graders with or at risk for mathematics difficulty. Remedial and Special Education, 1-11.

Fuchs, L. S., Schumacher, R. F., Long, J., Namkung, J., Hamlett, C. L., Cirino, P. T., … & Changas, P. (2013). Improving at-risk learners’ understanding of fractions. Journal of Educational Psychology, 105(3), 683–700.

Hamdan, N., & Gunderson, E. A. (2017). The number line is a critical spatial-numerical representation: Evidence from a fraction intervention. Developmental Psychology, 53(3), 587-596.

Rinne, L. F., Ye, A., & Jordan, N. C. (2017). Development of fraction comparison strategies: A latent transition analysis. Developmental Psychology, 53(4), 713-730.

Siegler, R. S., Thompson, C. A., & Schneider, M. (2011). An integrated theory of whole number and fraction development. Cognitive Psychology, 62(2011), 273-296.

Wellberg, S., Briggs, D. C., & Student, S. R. (2023). Big Ideas in the Understanding of Fractions: A Learning Progression. Boulder, CO: Center for Assessment, Design, Research and Evaluation (CADRE) at the CU Boulder School of Education.

Wilson, P. H., Edgington, C. P., Nguyen, K. H., Pescosolido, R. C., & Confrey, J. (2011). Fractions: How to share fair. Mathematics Teaching in the Middle School, 17(4), 230-236.

Practice 2       

Bailey, D. H., Siegler, R. S., & Geary, D. C. (2014). Early predictors of middle school fraction knowledge. Developmental Science, 17(5), 775-785.

Booth, J. L., Newton, K. J., & Twiss-Garrity, L. K. (2014). The impact of fraction magnitude knowledge on algebra performance and learning. Journal of Experimental Child Psychology, 118(2014), 110-118.

Braithwaite, D. W. & Siegler, R. S. (2021). Putting fractions together. Journal of Educational Psychology, 113(3), 556-571.

Fuchs, L. S., Malone, A. S., Schumacher, R. F., Namkung, J., & Wang, A. (2017). Fraction intervention for students with mathematics difficulties: Lessons learned from five randomized controlled trials. Journal of Learning Disabilities, 50(6), 631-639.

Fuchs, L.S., Newman-Gonchar, R., Schumacher, R., Dougherty, B., Bucka, N., Karp, K.S., Woodward, J., Clarke, B., Jordan, N. C., Gersten, R., Jayanthi, M., Keating, B., and Morgan, S. (2021). Assisting Students Struggling with Mathematics: Intervention in the Elementary Grades (WWC 2021006). Washington, DC: National Center for Education Evaluation and Regional Assistance (NCEE), Institute of Education Sciences, U.S. Department of Education. Retrieved from http://whatworks.ed.gov/.

Gaertner, M. N., Kim, J., DesJardins, S. L., & McClarty, K. L. (2014). Preparing students for college and careers: The causal role of Algebra II. Res High Educ, 55, 143-165.

Hansen, N., Jordan, N. C., Fernandez, E., Siegler, R. S., Fuchs, L., Gersten, R., & Micklos, D. (2015). General and math-specific predictors of sixth-graders’ knowledge of fractions. Cognitive Development, 35, 34 49. https://doi.org/10.1016/j.cogdev.2015.02.001

Hecht, S. A., & Vagi, K. J. (2010). Sources of group and individual differences in emerging fraction skills. Journal of Educational Psychology, 102(4), 843–859. https://doi.org/10.1037/a0019824

Jordan, N. C., Hansen, N., Fuchs, L. S., Siegler, R. S., Gersten, R., & Micklos, D. (2013). Developmental predictors of fraction concepts and procedures. Journal of Experimental Child Psychology, 116(1), 45 58. https://doi.org/10.1016/j.jecp.2013.02.001

Karp, K. S., Bush, S. B., & Dougherty, B. J. (2014). 13 rules that expire. Teaching Children Mathematics, 21(1), 18-25.

Ketterlin-Geller, L. R., & Chard, D. J. (2011). Algebra readiness for students with learning difficulties in grades 4-8: Support through the study of number. Australian Journal of Learning Disabilities, 16(1), 65-78.

Meert, G., Gregoire, J., & Noel, M.-P. (2010). Comparing the magnitude of two fractions with common components: Which representations are used by 10- and 12-year olds? Journal of Experimental Child Psychology, 107(2010), 244-259.

Mou, Y., Li, Y., Hoard, M. K., Nugent, L. D., Chu, F. W., Rouder, J. N., & Geary, D. C. (2016). Developmental foundations of children’s fraction magnitude knowledge. Cognitive Development, 39(2016), 141-153.

Resnick, I., Jordan, N. C., Hansen, N., Rajan, V., Rodrigues, J., Siegler, R. S., & Fuchs, L. S. (2016). Developmental growth trajectories in understanding of fraction magnitude from fourth through sixth grade. Developmental Psychology, 52(5), 746-757.

Rinne, L. R., Ye, A., & Jordan, N. C. (2017). Development of fraction comparison strategies: A latent transition analysis. Developmental Psychology, 53(4), 713-730.

Siegler, R. S. (2016). Magnitude knowledge: The common core of numerical development. Developmental Science, 19(3), 341-461.

Siegler, R. S., Duncan, G. J., Davis-Kean, P. E., Duckworth, K., Claessens, A., Engel, M., Susperreguy, M. I., & Chen, M. (2012). Early predictors of high school mathematics achievement. Psychological Science, 23(7), 691-697.

Torbeyns, J., Schneider, M., Xin, Z., & Siegler, R. S. (2015). Bridging the gap: Fraction understanding in central to mathematics achievement in students from three different countries. Learning and Instruction, 37(2015), 5-13.

Van Hoof, J., Verschaffel, L., & Van Dooren, W. (2015). Inappropriately applying natural number properties in rational number tasks: Characterizing the development of the natural number bias through primary and secondary education. Educ Stud Math, 90, 39-56.

Zhang, D., Stecker, P., & Beqiri, K. (2017). Strategies students with and without mathematics disabilities use when estimating fractions on number lines. Learning Disability Quarterly, 40(4), 225-236.

Practice 3

Ball, D. L., Ferrini-Mundy, J., Kilpatrick, J., Milgram, R. J., Schmid, W., & Schaar, R. (2005). Reaching for common ground in K-12 mathematics education. Notices of the AMS, 52(9), 1055-1058.

Bailey, D. H., Siegler, R. S., & Geary, D. C. (2014). Early predictors of middle school fraction knowledge. Developmental Science, 17(5), 775-785.

Braithwaite, D. W., Leib, E. R., Siegler, R. S., & McMullen, J. (2019). Individual differences in fraction arithmetic learning. Cognitive Psychology, 112(2019), 81-98.

Braithwaite, D. W. & Siegler, R. S. (2021). Putting fractions together. Journal of Educational Psychology, 113(3), 556-571.

Barnett-Clark, C., Fisher, W., Marks, R., & Ross, S. (2010). Developing essential understanding of rational numbers for teaching mathematics in grades 3-5. National Council of Teachers of Mathematics.

Fuchs, L. S., Malone, A. S., Schumacher, R. F., Namkung, J., & Wang, A. (2017). Fraction intervention for students with mathematics difficulty: Lessons learned from five randomized controlled trials. Journal of Learning Disabilities, 50(6), 631-639.

Fuchs, L. S., Schumacher, R. F., Long, J., Namkung, J., Hamlett, C. L., Cirino, P. T., … & Changas, P. (2013). Improving at-risk learners’ understanding of fractions. Journal of Educational Psychology, 105(3), 683–700.

Jordan, N. C., Hansen, N., Fuchs, L. S., Siegler, R. S., Gersten, R., & Micklos, D. (2013). Developmental predictors of fraction concepts and procedures. Journal of Experimental Child Psychology, 116(2013), 45-58.

Ketterlin-Geller, L.R., Powell, S., Chard, D., & Perry, L. (2019). Teaching Math in Middle School: Using MTSS to Meet All Students’ Needs. Baltimore, MD: Brookes Publishing.

Lortie-Forgues, H., Tian, J., & Siegler, R. S. (2015). Why is learning fraction and decimal arithmetic so difficult? Developmental Review, 38(2015), 201-221.

National Academies of Sciences, Engineering, and Medicine. 2001. Adding It Up: Helping Children Learn Mathematics. Washington, DC: The National Academies Press. https://doi.org/10.17226/9822.

Roesslein, R. I., & Codding, R. S. (2019). Fraction interventions for struggling elementary math learners: A review of the literature. Psychology in the Schools, 56, 413-432.

Siegler, R. S., & Lortie-Forgues, H. (2017). Hard lessons: Why rational number arithmetic is so difficult for so many people. Current Directions in Psychological Science, 26(4), 346-351.

Van de Walle, J. A., Karp, K. S., & Bay-Williams, J. M. (2016). Elementary and middle school mathematics: Teaching developmentally (9th ed.). Pearson.

Practice 4

Brown, G., & Quinn, R. J. (2006). Algebra students’ difficulty with fractions: An error analysis. Australian Mathematics Teacher, 62(4), 28–40.

Cramer, K., Monson, D., Whitney, S., Leavitt, S., & Wyberg, T. (2010). Dividing fractions and problem solving: Reflect and discuss. Mathematics Teaching in the Middle School, 15(6), 338–346. http://www.jstor.org/stable/41183034

Freeman, D.W., & Jorgensen, T.A. (2015). Moving beyond brownies and pizza. Teaching Children Mathematics, 21(2), 414-420.  https://doi.org/10.5951/teacchilmath.21.7.0412

Fuchs, L.S., Newman-Gonchar, R., Schumacher, R., Dougherty, B., Bucka, N., Karp, K.S., Woodward, J., Clarke, B., Jordan, N. C., Gersten, R., Jayanthi, M., Keating, B., and Morgan, S. (2021). Assisting Students Struggling with Mathematics: Intervention in the Elementary Grades (WWC 2021006). Washington, DC: National Center for Education Evaluation and Regional Assistance (NCEE), Institute of Education Sciences, U.S. Department of Education. Retrieved from http://whatworks.ed.gov/.

Hwang, J., & Riccomini, P. J. (2021). A descriptive analysis of the error patterns observed in the fraction-computation solution pathways of students with and without learning disabilities. Assessment for Effective Intervention, 46(2), 132–142. https://doi.org/10.1177/1534508419872256

Lortie-Forgues, H., Tian, J., & Siegler, R. S. (2015). Why is learning fraction and decimal arithmetic so difficult? Developmental Review, 38, 201-221. https://doi.org/10.1016/j.dr.2015.07.008

Newton, K. J., Willard, C., & Teufel, C. (2014). An examination of the ways that students with learning disabilities solve fraction computation problems. The Elementary School Journal, 115(1), 1–21. https://doi.org/10.1086/676949

Ni, Y., & Zhou, Y. (2005). Teaching and learning fraction and rational numbers: The origins and implications of whole number bias. Educational Psychologist, 40(1), 27–52. https://doi.org/10.1207/s15326985ep4001_3

Powell, S. R., & Fuchs, L. S. (2018). Effective word‐problem instruction: Using schemas to facilitate mathematical reasoning. Teaching Exceptional Children, 51(1), 31–42. https://doi.org/10.1177/0040059918777250

Powell, S. R., & Nelson, G. (2021). University students’ misconceptions about rational numbers: Implications for developmental mathematics and instruction of younger students. Psychology in the Schools, 58(2), 307–331. https://doi.org/10.1002/pits.22448

Schumacher, R. F., & Malone, A. S. (2017). Error patterns with fraction calculations at fourth grade as a function of students’ mathematics achievement status. The Elementary School Journal, 118(1), 105–127. https://doi.org/10.1086/692914

Siegler, R., Carpenter, T., Fennell, F., Geary, D., Lewis, J., Okamoto, Y., Thompson, L., & Wray, J. (2010). Developing effective fractions instruction for kindergarten through 8th grade: A practice guide (NCEE #2010-4039). Washington, DC: National Center for Education Evaluation and Regional Assistance, Institute of Education Sciences, U.S. Department of Education. Retrieved from whatworks.ed.gov/ publications/practice guides.

Siegler, R. S., & Lortie-Forgues, H. (2014). An integrative theory of numerical development. Child Development Perspectives, 8(3), 144–150. https://doi.org/10.1111/cdep.12077