Screening That Counts: Why Australia Needs Universal Early Numeracy Screening

Executive summary

Better early identification of students struggling with mathematics is a critical step in addressing underachievement

• Evidence shows virtually all students can reach proficiency in mathematics, if they receive systematic and high-quality instruction. But data from national and international testing shows too many Australian students are not meeting proficiency benchmarks. Those who fall behind often do so early in their school experience and rarely catch up.
• Successive reviews have advocated for better assessment tools for early identification of students at risk and subsequent intervention. In particular, screening tools that are administered to all students can ‘flag’ students who are at-risk of later difficulties with mathematics without additional support. For students needing additional support, the chances of positive outcomes are significantly higher when intervention is early and evidence-based.
• For intervention outcomes to be improved, a universal and systematic approach is needed for the early years of school. Effective early maths screening — particularly through a universal numeracy screener in Year 1 — could improve the opportunity for Australian students to be confident and successful in the subject.

Effective early screening measures should focus on robust models of number sense

• There are several early markers of students’ likelihood to experience difficulty in mathematics, including malleable skills such as ‘number sense’.
• Number sense represents a body of core knowledge about whole numbers, which predicts mathematics achievement and underlies the development of more complex mathematical skills and knowledge. Number sense encompasses the three domains of number (including saying, reading, and writing numbers), number relations (comparing and understanding numbers in terms of ‘more’ and ‘less’) and number operations (understanding and facility with addition and subtraction).
• Number sense is ‘teachable’ and students who receive quality early interventions in number sense can experience significant and lasting benefits.
• However, awareness of, and screening for, these key foundational skills is not systematically implemented in Australian schools. This means students at risk are not consistently identified early enough to maximise their chance of success.

Current student assessments in Australia do not meet adequate standards for universal screening

• Evidence shows effective maths screening approaches have some characteristics in common. Mathematics screeners must be efficient, reliable and directly inform teaching practice. Importantly, they must be designed to reflect research about the skills and knowledge that are most predictive of future maths success, so the right children are identified for additional support. Screening tools must classify children as ‘at-risk’ or ‘not at-risk’ with acceptable accuracy to enable support to be appropriately allocated to where it is needed.
• However, current approaches to early mathematics assessment do not represent an efficient or effective approach to ‘screening’. Tools currently in use are largely diagnostic in nature or measure achievement rather than risk. Such tools are important within a broad approach to assessment but were not designed and are not suitable for screening purposes.
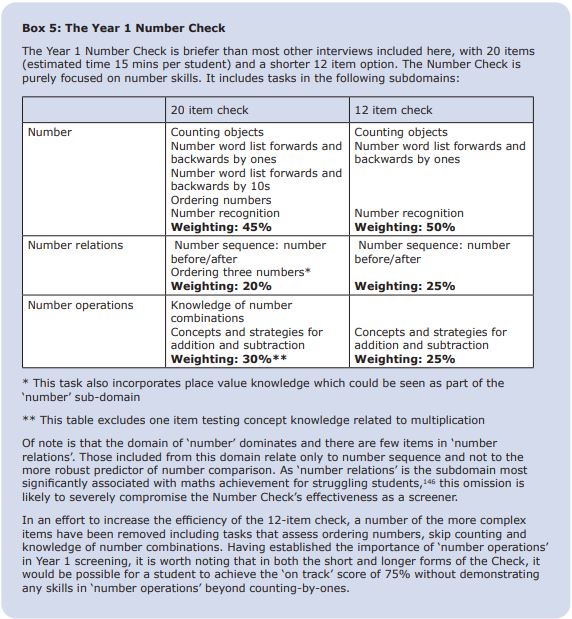
• The Year 1 Number Check, developed in response to previous recommendations for a consistent screening tool based on number sense in Year 1, is not widely used or fit for purpose in its current form. A new or significantly redesigned tool is needed which accurately represents the skills with predictive value in Year 1, is based on a robust model of what constitutes ‘number sense,’ and which measures not only knowledge and strategies but fluency with that knowledge. This tool should be research-validated to ensure its accuracy in identifying risk.

Policymakers should take action to widely implement effective screening and intervention

• Policy makers should implement a research-validated, nationally-consistent screening tool which measures aspects of the three domains of ‘number sense,’ consistent with the established research base.
• Screening tools designed on a conceptual model of ‘number sense’ should be developed for both Foundation and Year 1, and implemented with all students at least two times per year (beginning and middle of year).
  • The second testing period in Year 1 should be consistent across all Australian schools and used for central data collection.
  • A final testing period towards the end of Term 4 should involve a standardised test of maths achievement. This can help schools to evaluate how successful the teaching program has been and track students’ progress over time as they move through Primary School.
• Teachers and schools should be supported with professional learning programs to enable more intensive teaching for at-risk students. Systems should provide access to evidence-based tools for intervention, and the resources with which to deliver these to students identified through screening.
• Maths screening should occur within a multi-tiered framework which includes systematic processes for assessment and instruction at three tiers. Existing tools should be realigned to this framework, and progress monitoring tools developed.
• Early screening and intervention is necessary but not sufficient for some students to maintain pace with grade-level curriculum. Systematic screening and intervention resources and processes are also needed for middle and upper grades.

Introduction

International data have repeatedly shown many Australian school students struggle with mathematics. Around 10% of students achieve at a level that requires additional support (NAPLAN) or are below the international benchmark Trends in International Maths and Science Study (TIMSS) — which is the equivalent of around 400,000 Australian students per year. More than a quarter of 15-year-olds are low performers in the subject (see Figure 1).

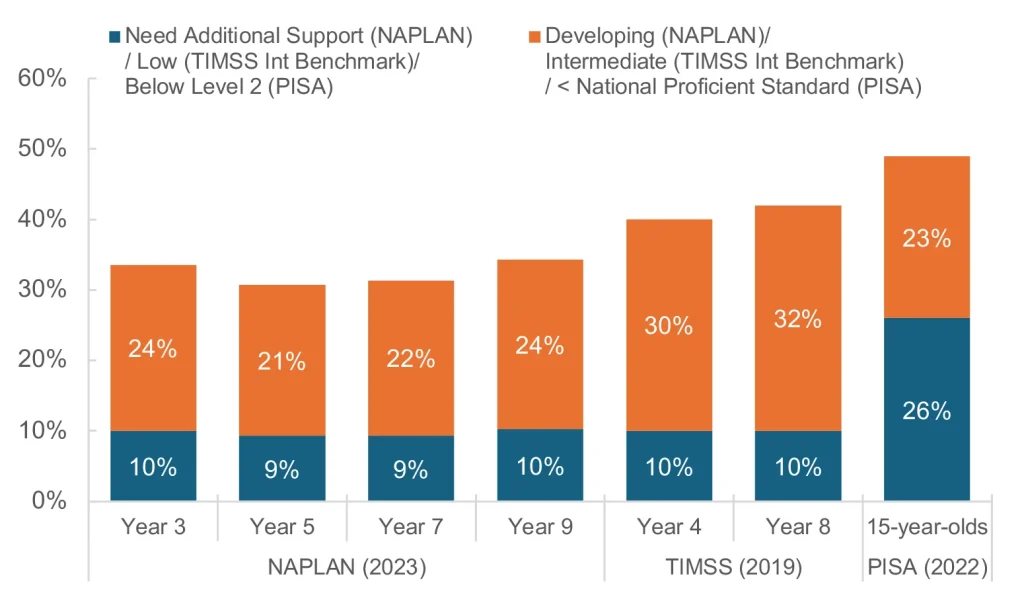
Figure 1: Proportion of Australian students achieving at levels below proficiency in domestic and international tests of numeracy and mathematical literacy

Australian students’ maths proficiency has at best stagnated (TIMSS, 2019)[1] — and at worst declined — both in absolute terms and compared to their overseas peers (Programme for International Student Assessment (PISA), 2022).[2] Over the most recent period of PISA testing (2018-2022), the gap between Australia’s lowest and highest achieving students continued to widen and is among the largest in developed countries in the world.

This cannot be attributed to a lack of money or instructional time. Australia spends around 23% more per student per year than the OECD average and requires the highest number of compulsory instructional hours in general education in the OECD.[3] It is abundantly clear that money alone is not the answer, and time spent in class does not necessarily equate to time spent well.

Students who struggle with maths can be identified early

Students who enter formal schooling with numeracy skills behind their peers rarely catch up, and mathematical risk factors can be evident much earlier than formal testing in school.[4] [5] [6] Students from disadvantaged backgrounds enter school with significantly lower number knowledge,[7] and are more likely to have slower rates of growth in their mathematical knowledge.[8]

Research shows that students’ pathways to post-secondary education are related to maths skills as early as age 4,[9] and can be predicted by their mathematics achievement in Year 5.[10] School mathematics achievement also has striking implications for life beyond formal schooling. Adults with poor numeracy have lower rates of employment, income, higher rates of homelessness and poorer health outcomes.[11] [12]  [13] It is estimated that around 1 in 5 adults do not have the numeracy levels required to successfully complete daily tasks such as reading a petrol gauge or managing a household budget.[14]

Research from the Productivity Commission and Australian Education Research Organisation (AERO) confirm the persistence of early difficulties with later academic skills. Basic literacy and numeracy skills upon school entry (as measured by the Australian Early Development Census) are strongly predictive of NAPLAN achievement in Year 3.[15] Students who perform poorly on NAPLAN in Year 3 are at high risk of continued poor performance throughout their schooling, with only one in five managing to later attain and maintain proficient levels of performance.[16]

Differences in early maths proficiency are associated with lower socio-economic status and with individual differences in cognitive abilities including working memory (the general capability of keeping small amounts of information active and accessible)[17] and attention. However, the quality of school preparation and instruction is a significant contributor to students’ outcomes.[18]

Lack of access to high-quality universal early numeracy screening

Screening in the initial years of schooling is an essential component of a coordinated response to increasing achievement in mathematics. By the time struggling students are identified by NAPLAN in Year 3, precious time has been lost and learning gaps become more challenging, expensive and unlikely to bridge.[19] [20] However, despite recent interest in early screening and intervention for numeracy difficulties, Australian schools and teachers routinely lack access to reliable tools and processes for identifying students at risk of later failure in school mathematics.

The need for consistency and rigour in such processes was recognised in 2017 by the National Advisory Panel for the Year 1 Literacy and Numeracy Check,[21] which recommended the development and use of a nationally consistent tool. This need was reinforced more recently by the Better and Fairer Review.[22]

Sadly, over the course of these six years, little change in practice and supporting policy has been implemented. As a result, current tools available to Australian schools are not designed for, or well suited to, universal screening procedures as recommended by the Better and Fairer Review.

Intervention outcomes have been mixed

Intervention outcomes have been mixed in practice, in part because they have not benefitted from high-quality universal screening. Policymakers have recognised the need to support students who are struggling or at risk of not meeting expected achievement levels. Interruptions to schooling due to the covid-19 pandemic resulted in the rollout of around a billion dollars in small group tutoring initiatives in NSW and Victoria to better support struggling students. Education ministers have further signalled the ambition to scale up such programs.

However, this willingness to better support struggling students through intervention has not been matched with improvements in valid and reliable ways to identify struggling students who would best benefit from targeted additional support. Namely, independent evaluations of government-run initiatives, while well intentioned, show that they failed to guarantee evidence-based approaches to assessment and intervention, and, as a result, unfortunately achieved no impact in improving student outcomes.[23]

Access to reliable data about who is likely to struggle in maths and what support they might need will help schools and teachers to intervene early and deliver more effective, targeted intervention. Despite the obvious need, approaches to early maths screening in Australian schools have changed little in the past 20 years, despite international research which has revealed much about how to gather such data in effective and efficient ways.

This report will examine research findings on effective screening processes for mathematics difficulties, and how current practices in Australia align with and could be improved by using the most recent scientific research into preventing and addressing numeracy difficulties.

The role of early mathematics screening

Detecting and addressing difficulties early can demonstrably impact achievement, anxiety, motivation and participation in mathematics, both in the short and longer term.

By identifying students who struggle early, and delivering high quality educational interventions, it is possible to alter patterns of underachievement.[24] [25] Providing quality educational interventions early in students’ schooling can raise achievement.[26] [27] In addition, students who master foundational skills in maths are better prepared to grapple with the more complex ideas presented in the later school years.

Much has been made of the issues in attracting students, particularly girls, into STEM subjects and fields. Anxiety around maths is often touted as the reason so many of these students avoid pursuing maths subjects and careers.[28]

Raising motivation and engagement have therefore been the focus of considerable effort and investment to address this issue by successive governments. It is certainly true that there is a complex relationship between issues around confidence, anxiety, self-concept, motivation and achievement.

However, recent research has revealed successful early mathematical experiences may hold the key. According to a recent CIS report from Professor David Geary:[29]

“Students who experience early difficulties with maths are more likely to suffer from maths anxiety, rather than the other way around.”

Hence, early difficulties are often the catalyst for a cycle of mathematics anxiety, poor motivation and underachievement. Therefore, effective mathematical interventions are likely to have flow-on effects not just to mathematical achievement, but also to motivation and interest — which influence choices about pursuing mathematics-related courses and careers. This is particularly the case for females, who disproportionately experience maths anxiety and are consequently underrepresented in secondary mathematics courses and mathematics-related careers.[30]

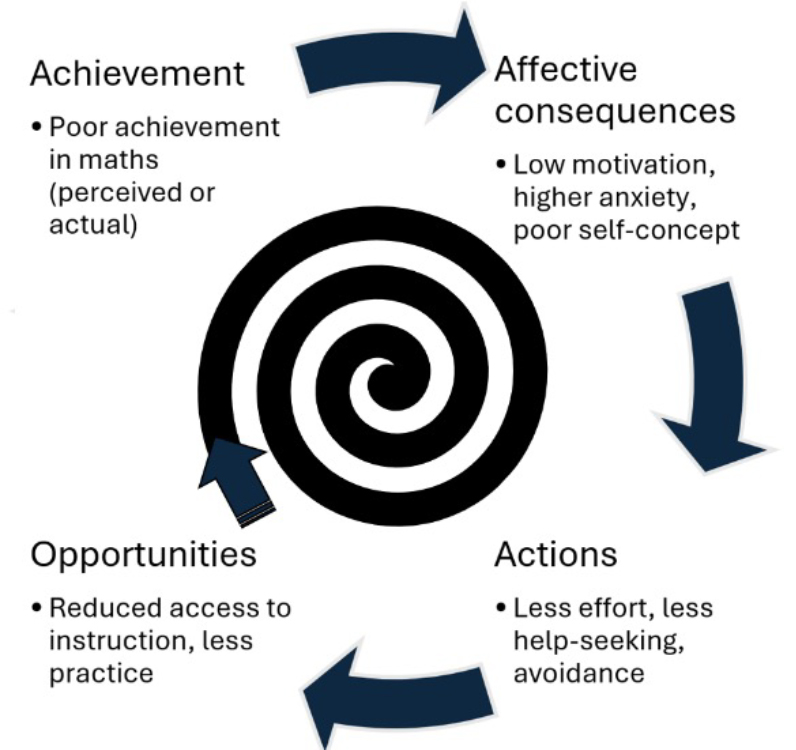
Figure 2: Representation of the failure cycle applied to mathematics

Students’ self-perceptions of whether they are any good at maths, known as self-efficacy, are a key factor in these decisions.[31] [32] It is hardly surprising that students who are anxious about maths and perceive themselves to be poor at maths will avoid mathematics subjects and maths-related careers. What is surprising is how early this negative spiral of poor achievement, low motivation, and poor self-efficacy becomes established [33] [34](see Figure 2).

In other words, the weight of evidence suggests that achievement creates motivation and engagement and reduces maths anxiety, rather than the other way around. Fortunately, by intervening early the impact of this destructive ‘feedback loop’ can be lessened. The importance of early intervention, therefore, cannot be over-emphasised. Students must receive mathematics support early and experience success with mathematics.

What tools are Australian schools using

Australian schools are well aware of the need to gather information about students’ early mathematical abilities to inform instruction. The primary methods by which systems currently collect this data is through individual interviews and standardised testing.

Most systems invest considerable amounts of time and money funding individual interview-style assessments in the early years of school. To conduct such interviews, relief teaching staff are usually employed to release classroom teachers who sit down with individual students and observe their responses to particular mathematical tasks. See Table 1 for an overview of commonly used assessment tools in early mathematics.

 

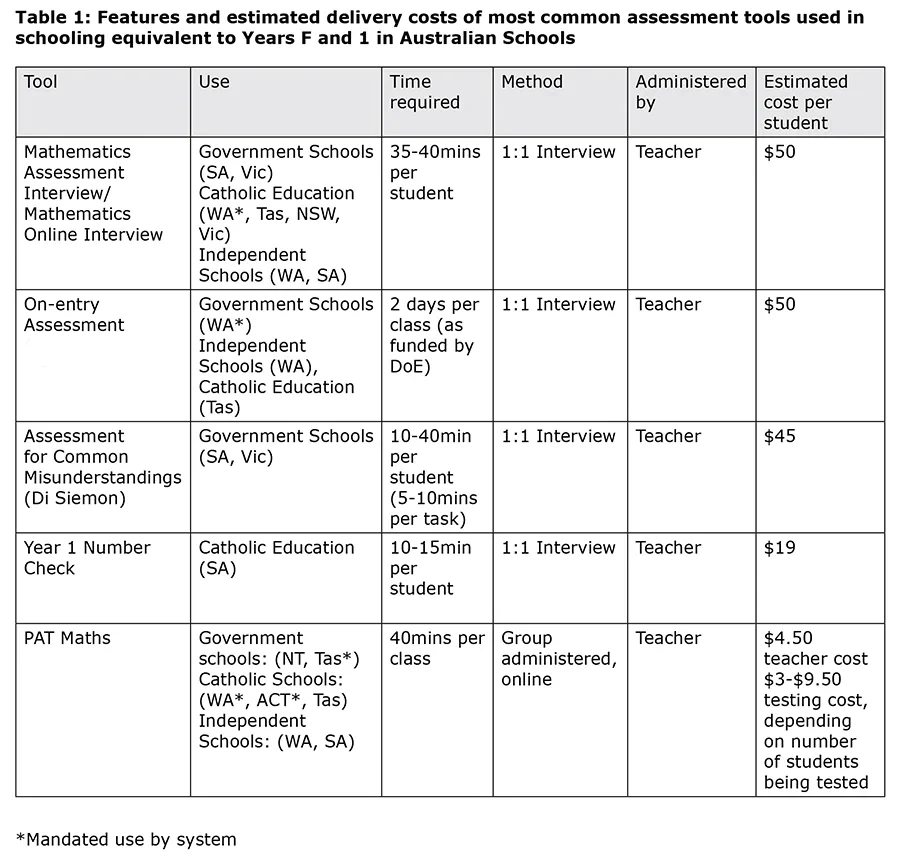
Two sectors in two different states indicated that they recommend their teachers use the Year 1 Number Check, developed by the federal government in response to the National Year 1 Literacy and Numeracy Check: Report of the Expert Advisory Panel.[35] See Box 1 for a brief description of the Year 1 Number Check.

The mathematics interview

Mathematics interviews have a long history in mathematics education, dating back to the research of Piaget in the early 1960s. Most, if not all, teachers would be familiar with Piaget’s ‘Stage Theory’ of cognitive development. This theory was derived through task-based clinical interviews in which children engaged with mathematical tasks while the researcher observed and asked questions to probe mathematical thinking and reasoning. Despite the subsequent inaccuracies uncovered in Piaget’s conclusions, clinical interviews are still highly valued by mathematics education researchers as a window into students’ thinking.

The clinical interview for mathematics has its origins in the traditions of cognitive science. In cognitive science, the focus is not on observable behaviour, but on uncovering the cognitive processes which underlie that behaviour. As Piaget expressed it:[37]

“Now from the very first questionings I noticed that though [the standardised] tests certainly had their diagnostic merits, based on the numbers of successes and failures, it was much more interesting to try to find the reasons for the failures. Thus I engaged my subjects in conversations patterned after psychiatric questioning, with the aim of discovering something about the reasoning process underlying their right, but especially their wrong answers. I noticed with amazement that the simplest reasoning task … presented for normal children … difficulties unsuspected by the adult.”

Researchers have learned much about children’s mathematical thinking through interview techniques. For example, it was through clinical maths interviews that Rochel Gelman and Randy Gallistel formulated their theory about the five principles that govern children’s successful counting of collections.[38]

Interviews are particularly favoured in approaches which aim to measure children’s progress along a trajectory of development in their thinking. The interview is the means by which teachers establish where the child is on that trajectory, and what they need to learn next.

For example, presented with the task, “I have 3 buttons and Mum gives me 6 more – how many do I have now?” there are a number of ways a child could represent and solve this problem. With access to counters (or indeed, fingers), a very young child could count out the 3 items, count out the 6 items, and then count the whole collections starting from one: 1, 2, 3… 7, 8, 9. A more advanced child might recognise they are able to start counting from the first collection, and count up to add the second collection: 3… 4, 5, 6, 7, 8, 9. More advanced still is the child who recognises that it is more efficient, and equally valid, to count up from the larger number: 6… 7, 8, 9. A further strategy would be to retrieve the known fact 3+6 from memory and know that the answer is “9” without any counting at all.

In perhaps the first comprehensive maths interview developed in Australia, Bob Wright and colleagues developed a number of assessment schedules based on such a framework: the Learning Framework in Number.[39] These interviews became the bedrock of the Mathematics Recovery intervention program for struggling Year 1 and 2 students.[40]  Mathematics Recovery was then adapted in the design of Mathematics Intervention which focused on at-risk Year 1 students.[41]

Inspired by this approach, in the following decades, large-scale projects based on understanding mathematical learning trajectories through diagnostic interviews were conducted in New South Wales (Count Me in Too), Victoria (Early Years Numeracy Research Project), and New Zealand (Numeracy Development Project). The success of these projects in raising teacher knowledge about mathematical development was largely attributed to the use of the interviews and the trajectories upon which they were based.[42] [43] The Early Years Numeracy Research Project (EYNRP) further demonstrated that this knowledge could have an impact on students’ learning, by moving them further along the trajectory when compared to peers outside the project.[44] The intervention program Extending Mathematical Understanding (EMU)[45] was developed as an intensification of the EYNRP for at-risk students.

Most individual mathematics interviews in use in Australia today are derived from these earlier projects. In particular, the Early Numeracy Interview (ENI) developed for the Early Years Numeracy Research Project[46]  was revised and expanded to become the Mathematics Assessment Interview (MAI)[47] which was then adapted for online delivery and renamed the Mathematics Online Interview for use in the Victorian Education system. The On-Entry Assessment – Numeracy used in Western Australia at the beginning of the Pre-Primary year (Foundation – Module 1) and Year 1 (Module 2) is also based on the ENI.

Standardised achievement testing

The school assessment landscape has changed considerably in the years since Count Me In Too and the Early Numeracy Research Project were active in schools. One significant change was the introduction of NAPLAN testing in 2008, after which the need to have a measurable way to monitor student progress through the years became a more pressing issue for schools. Education sectors in the ACT, NT, SA, Tasmania and WA indicated that their schools were required or encouraged to administer annual standardised mathematics achievement tests, most commonly ACER’s Progressive Achievement Test in Mathematics (PAT Maths).

PAT Maths aims to measure student achievement across all three strands of the mathematics curriculum (number and algebra; measurement and geometry and statistics and probability) and encompass all proficiency strands (fluency, understanding, problem-solving and reasoning).[48]

Standardised measures of achievement are generally acknowledged to be important for tracking students’ progress over time and prompting important discussions about student learning and educational policy.[49] [50] Some standardised achievement measures aim to provide extremely detailed information about individual students’ learning needs and involve individual administration over extended periods of time. However, the extent to which broad measures of curriculum attainment (e.g. PAT Maths, NAPLAN) are used by teachers to effectively inform instruction is less clear.[51]

Methods for early and universal maths screening

Teachers and schools need reliable data about who is struggling and what support they might need. However, this data must not come at an undue cost to instructional time. Therefore, there is a delicate balance to be struck between using tools that gather just enough data, just in time to be useful in informing support decisions.

The Better and Fairer Review[52] recognised the imperative that “students who start school behind or fall behind are identified as early as possible so they can receive targeted and intensive support” (p.57), and recommended the adoption of universal screening as a component of MTSS.  Increased consistency around screening processes in Foundation and Year 1 was recognised as an important first step.

Having established that teachers, schools and systems recognise the need for screening, it is necessary to consider what it is and how it differs from other forms of assessment. Australian schools already use a significant number of assessment processes in maths, but these processes are currently not preventing large numbers of children from falling behind and staying there.

Universal screening is better suited than diagnostic assessment for identifying students at risk

Universal screening, rather than diagnostic assessments, is required for effective identification of students in need of additional support. The value of universal screening has long been acknowledged internationally. In reviewing available research on supporting students with mathematical difficulties, the leading recommendation of the 2009 report of the Institute of Education Sciences[53] was that:

“…schools and districts systematically use universal screening to screen all students to determine which students have mathematics difficulties and require research-based interventions.”

The ‘universal screening’ paradigm was first developed in preventative medicine. Universal screening procedures in health have a long history of research and successful implementation and are a useful analogy for developing processes in education. According to the National Library of Medicine (USA):[54]

“Diagnostic tests are usually done to find out what is causing certain symptoms. Screening tests are different: they are done in people who do not feel ill. They aim to detect diseases at an early stage, before any symptoms become noticeable. This has the advantage of being able to treat the disease much earlier.”

Whereas the purpose of diagnostic assessment is to identify the potential causes (and by extension possible treatments) for specific known problems, the purpose of screening is to identify problems before they might be obvious to treatment providers or even patients themselves. Screening tests are administered across entire populations to determine who may be at-risk of an adverse outcome (in this case, poor achievement). For example, health systems schedule regular visits for new mothers and their babies to the child health nurse. At these visits, children are routinely weighed and measured and vital signs are collected. These measures are valid universal screenings that are used to signal a potential problem in development that merits further identification and possibly treatment efforts.

In other words, the purpose of screening is to identify which children need further assessment and possibly intervention. The purpose of diagnostic assessment is to figure out which intervention is needed. The reason year-end test scores are not effective universal screening devices is that year-end tests occur after instruction has been delivered and reflect whether that instruction was effective or not in hindsight. Screening measures, in contrast, are designed to be given midstream when intervention actions can be initiated to avoid or prevent failure on the year-end measure. Screening measures serve two important purposes in assessment: they are used to evaluate general programs of instruction for the purpose of program improvement and they are used to signify the need for intervention for most students, small groups of students, and individual students.

Therefore, the small distinction between ‘screening’ and ‘diagnostic’ assessments is an important one. Early identification through screening has also been a goal of reading research, although over a more extensive period of time, resulting in the design of efficient tools for identifying students at-risk which are then supplemented by more detailed diagnostic measures to inform intervention decisions. Many have suggested it is now time to apply what we have learned about screening in reading to screening for maths difficulties.

Early screening must be part of a systematic approach

In order to change students’ long-term learning trajectories and outcomes, we need to change the way schools identify and offer targeted support to those most at risk. There will be no magic panacea or ‘quick fix’ that will catch struggling students up and keep them achieving at the desired level. A complex problem requires a multi-tiered solution; specifically, evidence-based strategies and tools from the moment students walk into their first classroom and every year thereafter.

Many researchers and education systems around the world, including Australia, are now recognising the value of Multi-Tiered Systems of Support (MTSS) to ensure all students receive the level of support that will enable them to succeed. As asserted by the Better and Fairer Review,[55] “implementing a multi-tiered system of supports will lift achievement for all students” (p.54). In a recent report, the Australian Education Research Organisation recommended MTSS as the most effective framework for identifying and supporting struggling students in Australia.[56]

An MTSS gives an enabling context in which early screening and intervention can be successful in changing educational outcomes for students. Struggling students receive progressively more intensive support to ensure everyone’s needs are met. Support and resourcing is allocated on the basis of educational need and regardless of classification – socio-economic, disability, ethnic or otherwise. At each layer of intensity, instruction is informed by and monitored with targeted assessment tools. In the first instance, this assessment begins with an effective screening tool that can be used with whole classes of students to give reliable information about who needs extra support, and a starting point for what that support should look like. Figure 3 shows the three levels, or ‘tiers’ of cumulative support that are integral to MTSS. MTSS is described in more detail in Box 2.

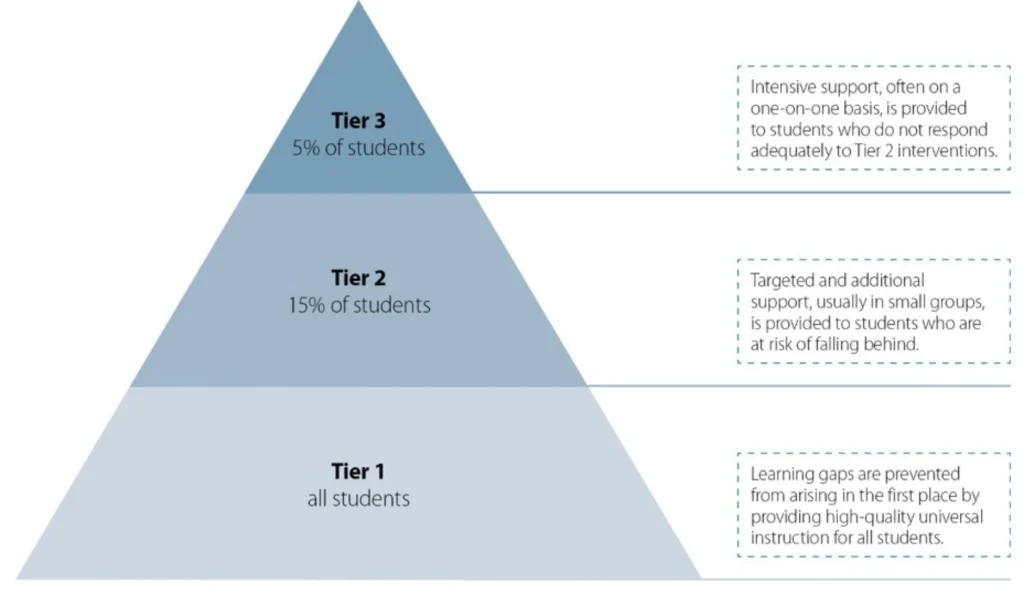
Figure 3: MTSS model showing a coordinated system of increasingly intensive support offered in three ‘tiers’. Source:  the Better and Fairer Review

A Multi-Tiered System of Support (MTSS) begins with a high-quality, evidence-based core curriculum for all students. A core component of this instruction for all, referred to as “Tier 1”, is the use of efficient, accurate and reliable tools (universal screening tools) for identifying students at risk of or experiencing difficulties. In Australia, a recent move towards embracing the science of reading has led to the widespread adoption of universal screening tools which identify students struggling in reading, such as the Year 1 Phonics Screening Check, but as this report will attest, there is currently no comparable approach to early screening in mathematics.

Instruction is intensified for those students identified through Universal Screening. Some researchers have recommended classwide instructional intensification as a “Tier 1.5”, which sits between the first two tiers for populations where many students are identified as ‘at-risk.’[57] Once ‘at-risk’ or struggling students are identified (or fail to respond to classwide intensification where this is applied), schools need clear processes for intensifying instruction for those students so that they can ‘catch up’ to their peers. Reducing group size is a common way of providing intensification, and Tier 2 small group support applies the same evidence-based principles of instruction as the core curriculum in Tier 1, but is more intensive. Instruction at each tier is cumulative, and occurs in addition to, and not instead of, high quality instruction at previous tiers. Assessment tools have an important role to play in Tier 2, with detailed diagnostic assessments helping teachers identify specific areas of difficulty and choose focuses for intervention. Progress monitoring assessments serve an important role in informing decision making regarding whether interventions are working or need to be altered/intensified/supplemented with yet more intensive interventions (Tier 3).

Most students receiving Tier 2 instruction are able to use this more intensive support to “catch up” with their peers. A small minority require the further intensification of support in Tier 3, which may involve very individualised work on foundational skills in addition to the other tiers. These students often have neurological reasons for their difficulties such as disabilities or Specific Learning Disorders. Diagnostic assessments are used in Tier 3 to inform planning and progress monitoring tools are used with greater frequency to check students are making expected progress.

Existing early screening approaches based on Number Sense

At this time, examples of empirically validated screening measures focused on ‘number sense’ are found only overseas (a detailed description of number sense is provided later in this report). Although many effective screening tools include tasks aligned to some or all of the three subdomains of ‘number sense’, there are also examples in which a conceptual model of ‘number sense’ is central to the design of the screener as a whole.

One example of this is the Number Sense Screener (NSS)[58] for use in Kindergarten and early Grade 1, and the Screener of Early Number Sense (SENS) which has broader application across Preschool to Grade 1.[59] As these tools were developed and researched in the USA, Kindergarten in North American education systems could be considered equivalent to Foundation in Australia (pre- Year 1). The SENS acknowledges the different mix of competencies important in each grade level. Both screeners have shown good accuracy in classifying children as at-risk or not at-risk for mathematics difficulties, and are designed to channel children into intervention programs such as the associated Number Sense Interventions.[60]

The same framework informed the design of the Early Mathematical Assessment (EMA@School) from Carleton University which has been widely trialled in Canadian schools. Although the EMA has been trialled across Kindergarten (Australian equivalent to Foundation) to Grade 4, and used to identify children for intervention and to monitor their progress, data on reliability and validity is yet to be published.

The Early Numeracy Screener (ENS) applied a similar framework around core mathematics competencies for 5-8 year-olds to screen First Grade children for mathematics difficulty. This framework was structured around four core domains, with number knowledge separated into symbolic and non-symbolic number sense and counting skills.[61] The ENS was found to be a valid measure of early number competency and correlated with end-of-year national test results.[62] [63] While developed at the University of Helsinki in Finland, the screener and subsequent First Grade intervention showed promise when trialled in South Africa.[64]

Characteristics of effective screeners

There are a number of practical considerations when designing or choosing screening measures for broad use across large populations of students. As explained by the 2009 report of the Institute of Education Sciences:[65]

“Schools should evaluate and select screening measures based on their reliability and predictive validity, with particular emphasis on the measures’ specificity and sensitivity. Schools should also consider the efficiency of the measure to enable screening many students in a short time.” (p.13)

Screening tools should detect children at risk of mathematical failure, in ways that are reliable, accurate, and inform instructional decisions in clear and productive ways.

Reliability

The above quote reveals a number of important characteristics of screening tools. Firstly, scores must be reliable, meaning the tool gives consistent results that can be applied broadly across diverse populations. There are different forms of reliability; for example, test-retest reliability (a student tested on the measure is likely to receive a very similar score if they were to sit the test a week later), internal consistency (how well scores from a set of items relate to each other), alternate forms reliability (how well scores on different sets of items within the screener relate to each other) and inter-rater reliability (how similarly different scorers rate the same responses). Measures of early maths validated by research typically rate moderately-strong to strong for reliability; both in timed and untimed presentations.[66]

Predictive validity

Secondly, scores must have strong ‘predictive validity’, meaning they are a good indicator of later maths achievement. The following sections have an extensive review of those skills and competencies which show predictive validity for maths achievement.

Sensitivity and specificity

Specificity and sensitivity are important to ensure that scarce additional resources are allocated where they are actually needed — to the children who would have struggled without the additional support. Sensitivity refers to the degree to which the tool is accurate in identifying children who will go on to have difficulty, and specificity to ruling out children who will not.

Research has revealed the latter is a significant problem in early maths screening. In order to avoid missing anyone, even measures considered to have ‘good specificity’ still identify large numbers of false positives.[67] These children are ‘flagged’ at the screening stage as being ‘at-risk’ but manage to ‘catch-up’ without the need for additional support — meaning scarce intervention resources may be directed inefficiently, thereby reducing the intensity available for students who really need the help.

Gated screening is more accurate than at a single-point-in-time screening

One solution to this problem is the use of a ‘gated’ screening process in preference to a single point in time. Gated screening processes require that schools consider multiple sources of information in making intervention decisions.  Students identified through the initial ‘gate’ (screen) as being ‘at-risk’ have the opportunity to benefit from increased instructional intensity in the regular classroom.[68] This increased intensity means increased opportunities to respond, which can be achieved through more direct instructional approaches with frequent group responding and/or carefully structured peer practice protocols.

Only those students ‘at-risk’ through the first gate are then tested for the second ‘gate’ (see Figure 4). This identifies students who have failed to respond to the increased intensity, and are therefore likely to need additional support to ‘catch up.’

 

Figure 4: Representation of ‘gated screening’ process

In order to maximise accuracy, this second ‘gate’ ideally features a measurement instrument different from the first.[69] [70] In measuring number sense, the second gate could have an exclusive or heavier focus on those skills which research has revealed are most predictive for low-achieving children in a given year level. For example, although a universal screener (gate one) for Year1 may feature all three strands with a relatively heavier focus on number relations and number operations, the second gate may focus increasingly on number relations (comparing number symbols or number line estimation), which is especially significant in predicting the achievement of lower achieving students at this age.[71]

Alternatively, the two gates can focus differentially on sensitivity and specificity to increase decision accuracy.[72] In a context where only one reliable screening tool may be available, cut scores with the same ‘number sense’ tool could be manipulated to prioritise sensitivity at the first gate and specificity at the second. In this approach, a wider net is cast at the first gate to minimise the chance of students being ‘missed’ by the screener. Following a period of intensified instruction, the screener is re-administered to only ‘at-risk’ students with a more selective cut-score to rule out those students who have benefited from that instruction and do not require further support at this time.

The underlying principle of gated screening is to triangulate multiple sources of data that measure both the acquisition of predictive skills and knowledge, and the impact of classroom instruction on areas of difficulty. When implemented effectively, gated screening results in more accurate classification decisions than ‘single point in time’ screening, especially where there is a high base-level of risk in a student population; i.e. many students are likely to be identified as at-risk.[73] [74] Where gated screening leads to increased instructional intensity after the first gate, this benefits all students in addition to improving the functioning of the screening.

Efficiency

Because education systems, like health systems, have scarce resources: [75]

“[they] are faced with opportunity costs; this means that any investment in a screening tool will come at the cost of other health services to the detriment of those patients who would have been treated”

Time and money spent testing is time not spent teaching, just as resources spent on health screening are therefore not available for patient care. Hence, screening tools must be efficient.

Informing instructional actions

There is one further lesson from health which has direct relevance to education:[76]

“… treating a disease at an early stage only makes sense if it leads to a better health outcome than treating it at a later stage.”

Access to educational screening tools which lead to specific instructional actions is similarly important in raising achievement. In a synthesis of 21 research studies concerning students with special needs (which in the USA includes those with Specific Learning Disorders in reading, writing and mathematics), it was found that systematically collecting data to inform instruction increased achievement generally. However, the effects were twice as large when teachers attended to decision rules made before the assessment was administered, rather than using their own judgement to decide how to respond to the results afterwards.[77] Therefore, effective screening tools should have clear decision rules and lead to particular instructional actions.

Two main schools of thought in predicting early numeracy success

The first task is to determine the skills and abilities which should be the focus of screening tools, as most predictive of mathematical success. The goal of screening is to identify those students who, without additional support, would likely go on to score below proficiency levels in subsequent tests such as NAPLAN and TIMSS. This information then enables schools and teachers to appropriately target support.

Efforts have primarily come from two fields: cognitive psychology and behavioural psychology.

Cognitive psychologists are focused on numerical cognition: the neural and cognitive mechanisms underlying our ability to understand and use numerical information.[78] Thus, relevant research from this field has focused at least in part on the search for a ‘core deficit’ that underlies later difficulties in numeracy.

It has long been established that what we refer to as ‘learning’ is the result of complex interactions between internal characteristics and environmental conditions. Although we all learn with the same cognitive architecture, there are significant differences between individuals in the functioning of this architecture. These differences can affect the ease with which we acquire the knowledge and skills that schools are tasked with teaching to children. When such a difference has a significant impact on the learning of a core body of knowledge such as reading or mathematics, it can be described as a ‘core deficit.’

In early reading assessment, a significant body of research and practice has concluded that phonological processing (proficiency in processing the sound structure of language) represents a ‘core deficit’ because this capability enables the acquisition of a cascade of skills needed for proficient reading. However, there is unlikely to be one single ‘core deficit’ in mathematics that is responsible for poor mathematics achievement. The core skills and knowledge for mathematics change as the demands and nature of mathematics change throughout schooling.

In contrast to the cognitive psychologists’ approach, behavioural psychology focuses on learning as an observable change in behaviour in response to environmental stimuli.[79] Hence, this research focuses on the measurement of learning at different stages of schooling and on measuring growth in response to instructional conditions.

In mathematics, unlike reading, it is unlikely there is a single General Outcome Measure — a quick and reliable indicator of overall competency — that is valid in measuring mathematics achievement across time. The skills most representative of overall maths achievement, and most predictive of future maths achievement, differ depending on stage of learning and therefore schooling.

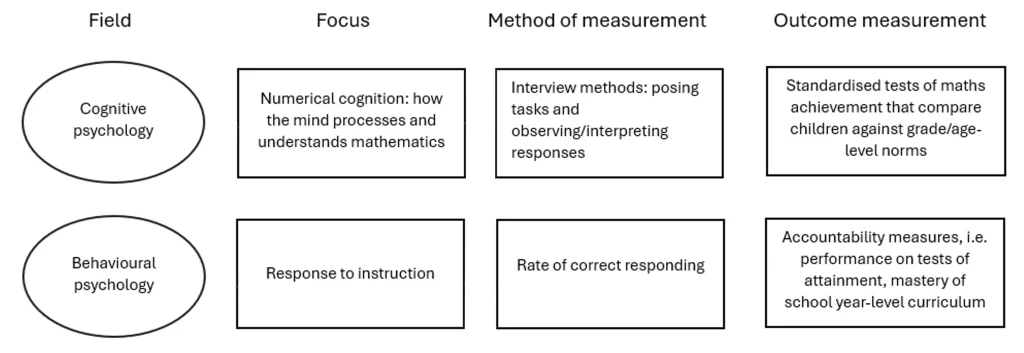
Figure 5: Schematic representation of the approaches of cognitive and behavioural psychology fields to screening research in mathematics

Cognitive psychology: The search for a core deficit

The search for a core deficit in numeracy parallels the work done in literacy which has revealed that phonological processing deficits (sensitivity to and use of the sound structure of spoken language, which includes the ability to isolate individual sounds in speech) appear to be at the root of most reading difficulties.[80] Research on early literacy learning has consistently revealed the importance of skills related to the mapping of letters and letter combinations onto these sounds for early literacy instruction.[81] [82] [83] These mapping skills are reliable predictors of early reading development, which has aided the development of tools for identifying students at risk of difficulties such as the Year 1 Phonics Screening Check.

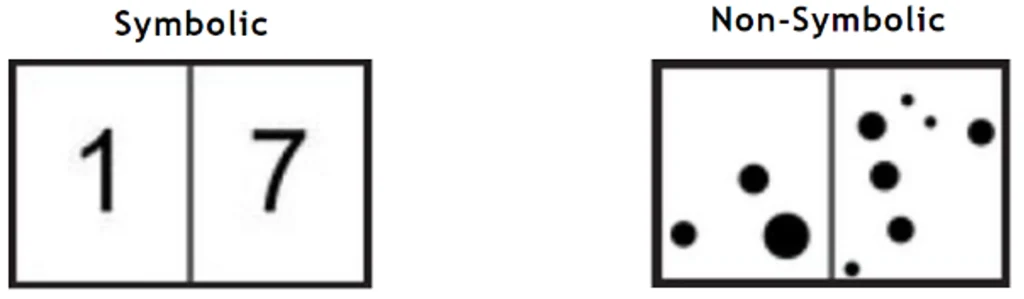
Figure 6: Sample of symbolic vs non-symbolic comparison tasks from the Numeracy Screener (Numerical Cognition Laboratory, 2024)

Cognitive psychologists have attempted to learn about the core components that enable skill with numbers, largely using individual interview techniques. Symbolic number processing and the Mental Number Line have been investigated as possible candidates for a core deficit in numeracy, enabling children to understand abstract mathematics. The speed at which children process (compare) numerals (and not quantities, i.e. shown with dots)[84] is predictive of their future success with mathematics. This ability is thought to rely on a mental structure called a Mental Number Line.

The human mind has been shown to develop a spatial representation of numbers, on a line with smaller numbers on the left and larger numbers on the right.[85] While humans are born with certain quantitative abilities, the development of an increasingly accurate mental number line occurs in response to formal mathematics instruction and is thought to enable students to learn arithmetic[86] and even underlie later success with fraction concepts and procedures.[87] This spatial representation of number magnitude is at least partly responsible for the strong relationship between early spatial abilities and mathematics development.[88] [89]

In the early years of schooling, students’ mental representation of the number line overestimates the distance between smaller numbers and compresses the distance between larger numbers. The development of a more linear mental number line where values are equally spaced has been shown to be reliably related to mathematics achievement in the early years of school  (see Figure 7).[90] [91]

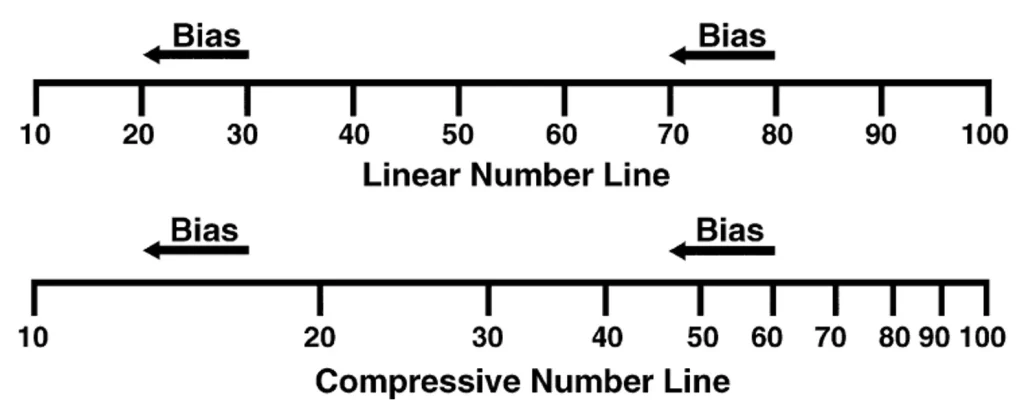
Figure 7: Linear vs non-linear representation of a number line (make a version of this which starts from zero and is more logarithmic without the ‘bias’ labels)

There is conflicting evidence as to whether a deficit in number magnitude processing is unique to students with persistent mathematical difficulties, diagnosed as Mathematical Learning Disabilities or a Specific Learning Disorder in Mathematics.[92] [93] Although number line representations remain important, these same skills have very little influence on students’ mathematics achievement by the time they reach upper primary school.[94] While whole number knowledge and arithmetic are most important in the early grades, fraction knowledge is a key predictor in later grades.[95]

Behavioural psychology: The search for a General Outcome Measure

Behavioural psychology has largely focused on the development of tools known as Curriculum-Based Measurement (CBM). Due to the need for measures to detect growth in response to instruction, CBMs have a heavy focus on measuring fluency as indicated by rate of correct responding (measures are timed). The fluency with which a skill is performed is related to the student’s stage of learning within an instructional hierarchy which begins with acquisition and progresses to fluency building and finally mastery – enabling retention and application of the learned skill.[96] Therefore, measuring the rate at which a skill is performed can give insight into whether the student is still acquiring the skill, is ready for independent practice, or has mastered it and is capable of applying it across contexts.

In reading, acquisition and mastery of the alphabetic code knowledge for reading and spelling is the gateway to students engaging productively with text. It facilitates the application of higher level skills such as reading comprehension and written composition. This means that, across a broad range of ages, a single measure of oral reading fluency (ORF: measured as words read correctly per minute on a grade level text) can be used as a General Outcome Measure (GOM) — a quick and reliable indicator of overall reading achievement. Such measures are very useful for screening for early difficulties, and efficiently monitoring progress over time including all the grade levels during which children are learning to read. In reading, educators can use a brief oral reading fluency measure to gain reliable information about students’ overall reading progress, in the same way a doctor might take your temperature to see if you have an infection (but without revealing the source or nature of the infection).

However, in mathematics education, the search for a single GOM has not been successful. While some researchers have developed measures that sample across the different skills and concepts taught in each year-level curriculum to attempt to monitor progress, [97] concerns have been raised about the measures’ sensitivity in detecting early difficulties.[98] In order to measure growth across the year, these measures must necessarily include a large amount of content that has not yet been taught, meaning many children are expected to score poorly in the first half of the year. This creates a ‘floor effect’ in the data or a restricted score distribution that weakens the sensitivity of the scores to reflect risk. The incapacity of these scores to reflect risk in the first half of the year is especially problematic because that is when the risk decision is most critical while there is time to deliver intervention. Further, because the measures include such a broad range of skills, they are incapable of detecting short-term growth from instructional interventions which may only focus on a very small subset of what is tested on a GOM.

One solution to this challenge has been the use of Mastery Measurement to measure the acquisition of more specific sets of skills.[99] Such measures have been referred to as ‘Goldilocks measures’ and have been shown to be highly reliable for identifying more global mathematics risk.[100] Further, such measures are highly sensitive when used for screening[101] and intervention progress monitoring.[102] Mastery measurement requires that skills targeted for assessment must be closely related to the skills expected to be mastered during the course of the instructional year. When a student reaches mastery on a given assessment, then the assessment should progress to the next logical benchmark skill.

An example of skills targeted for Mastery Measurement in early levels of the SpringMath program is shown in Figure 8.

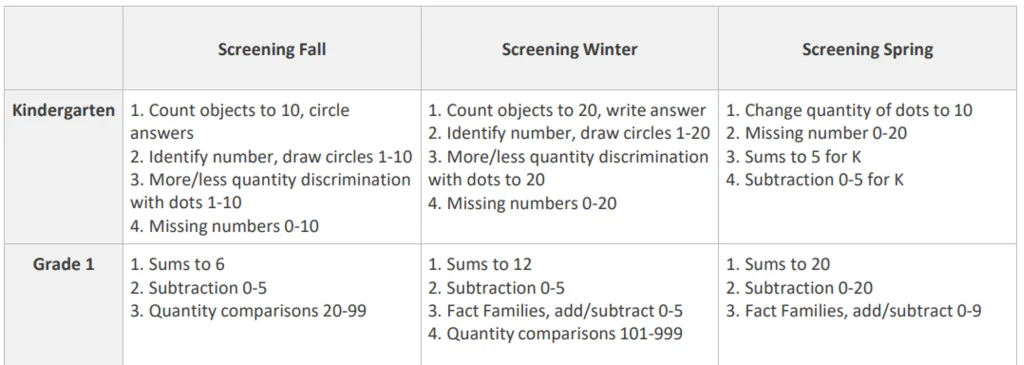
Figure 8: Skills targeted for screening in SpringMath (from www.springmath.com)

Measuring aspects of ‘number sense’ in the early years of primary school can effectively guide early maths screening

Despite different methodologies, both cognitive and behavioural psychology fields have come to remarkably similar conclusions regarding the maths skills and knowledge that predict later achievement. In particular, a number of recent systematic reviews and meta-analyses bring together the conclusions of hundreds of studies involving thousands of children.

Although the measures used by different researchers are varied, they are consistent in their attention to three interrelated bodies of knowledge about number. These same ‘subdomains’ reflect both what children know and understand and what they are able to demonstrate to inform decision making. These key aspects of core number knowledge and skill were identified by the National Research Council (NRC) in their comprehensive report Mathematics Learning in Early Childhood: Paths towards excellence and equity.[103] They are number, number relations and number operations, all of which contribute both independently and collectively to predicting future mathematical success.[104] [105] They have collectively been termed ‘number sense.’

‘Number sense’ is generally acknowledged to be essential for success in early mathematics. The term, however, means different things to different people in different fields. While the report of the Expert Advisory Panel on the National Year 1 Literacy and Numeracy Check[106] recommended ‘number sense’ as a focus for screening and emphasised its importance, they did not define it in any operational way. This review of the literature therefore builds on that earlier recommendation by defining number sense and the components which predict mathematical achievement.

‘Number sense’ is a popular but somewhat ‘muddy’ term. Some use it to describe the intuitive knowledge about number we have from infancy, termed ‘biologically primary’ knowledge, and others as a more complex set of competencies involving numerical reasoning and reliant on instruction, known as ‘biologically secondary’ knowledge.[107] Nevertheless, it is a useful construct due to the large amount of research that exists about its components and its high visibility as an essential component for screening and instruction. For the purposes of this report, ‘number sense’ describes the three domains of number, number relations and number operations discussed above and represented in Figure 9.

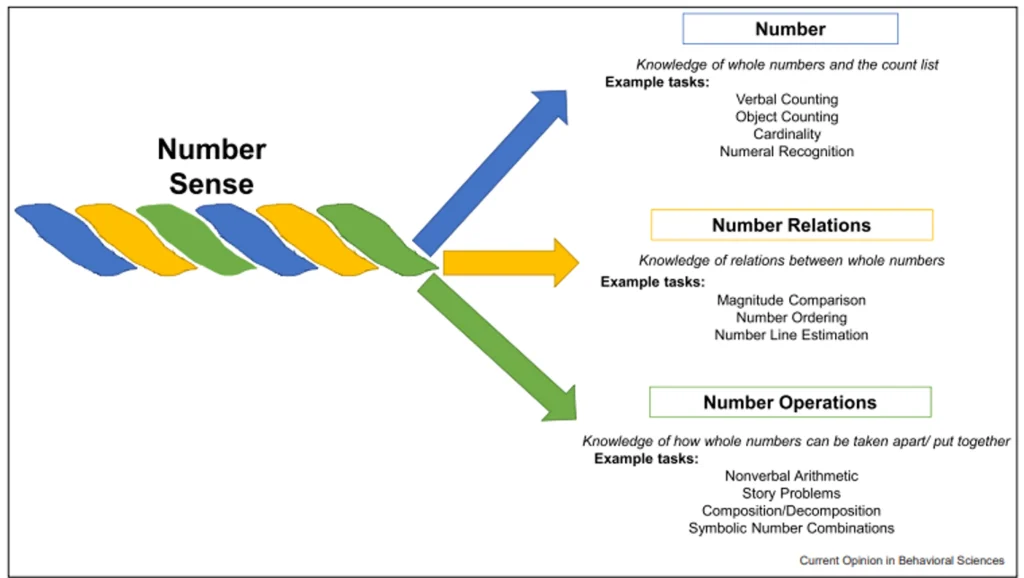
Figure 9: Components of Number Sense as visualised by Jordan, Devlin and Botello. Source: Core foundations of early mathematics: refining the number sense framework. Current Opinion in Behavioral Sciences (2022)

The National Research Council’s three domains of number, number relations and number operations are a useful framework through which we can examine measures which effectively predict mathematics achievement.

Number

According to the NRC, ‘number core’ knowledge includes the ability to recognise and write number symbols, match these to sets of objects and understand principles that govern counting. Key skills are having fluency with the number word list, one-to-one correspondence and cardinality (see Box 3 for explanations).  A number of these aspects of number knowledge are reliable predictors of later achievement. Children’s counting skills including reciting number sequences, filling in missing numbers from sequences of numbers, counting sets and showing awareness of the principles which govern counting, predict later achievement,[108] [109] [110] with progression through a skill hierarchy reflecting more sophisticated strategies (e.g. counting from a number other than one) more predictive in the long term than simple counting.[111]

The ability to accurately identify and write numbers, usually single digit numbers, is a useful measure particularly in the early years.[112] [113] [114] Subitising – the ability to recognise small sets of objects without counting – has also been identified as a useful predictor in studies focused on the preschool years.[115]

Number relations

The number relations subdomain concerns the comparison of quantities and numbers, and reasoning in terms of more, less and the same. Cognitive scientists have focused significantly on measuring both informal, approximate systems of number and more accurate representations of a mental number line. In measuring the accuracy of the informal abilities, known as the Approximate Number System (ANS), children are asked to judge the greater of two collections of dots, with the task becoming harder as the ratio of the values decreases. The ANS has shown value in predicting mathematics achievement, but not to the same extent as more formal, exact and symbolic systems for comparing number such as comparing numerals to say which is more, or plotting a number accurately on a ‘bounded’ (marked at both ends) number line.[116] [117] [118] [119] Examples of these tasks are shown in Box 4.

Number operations

The subdomain of number operations includes working with physical objects as well as mental representations of quantities and working solely with number symbols. Some studies have shown that even before students are able to work with number symbols, their nonverbal calculation abilities are related to future mathematical success.[120] [121] [122] For example, shown a collection of three counters which is then covered by a box, the child observes the interviewer putting another counter underneath the box and then is asked how many will be under the box now. Students can respond either verbally or by making/identifying a collection the same size as the one that is under the box. This minimises the influence of language skills on performance. Following the start of formal schooling, the utility of timed written measures of addition and subtraction with single digits to predict maths achievement has a strong research base.[123] [124] Box 4 contains examples of tasks that have been used successfully in screening to measure number operations skills.

General considerations for universal maths screening

Composite measures or single skill measures

The research reviewed that a broad range of skills and competencies can be used to predict maths achievement. Surprisingly, screeners that sample a broader number or range of measures are not necessarily more accurate in classifying students’ at-risk status. Especially in the primary school grades, it is possible to predict maths achievement with reasonable accuracy with carefully targeted single-skill mastery measures,[126] although some research cautions that single skill measures have a tendency to over-identify risk.[127]

The brevity of such an approach would certainly be appealing from an efficiency point of view. In fact, instructional programs based on sequences of carefully planned brief measures have been highly successful in identifying struggling students and raising achievement.[128] However, in the absence of such a systematic approach in Australia, overly brief measures may provide insufficient information to inform teaching in productive ways. Selecting a screening approach for Australian schools that will positively influence instructional emphases in addition to identifying at-risk students is a high priority.  Multiple-skill measures structured around a teachable construct such as ‘number sense’ are likely to have a greater positive impact on the instructional practices of Australian teachers.

Different skills are predictive at different times

Although the measurement of skills and knowledge in the three domains referred to above as ‘number sense’ is predictive across the early years of school, the relative value of each changes depending on schooling level/age. While simpler skills such as knowledge of the counting sequence, number magnitude and number identification are strong predictors in the early years of school, calculation and word problem-solving are stronger predictors in the Primary School grades.[129]

Similarly, the predictive value of different skills is dependent on student expertise, with lower achievers in the early years more influenced by number knowledge and relations, and higher achievers by skills in number operations.[130] This reflects the fact that learning in mathematics is hierarchical, with the development and application of more complex skills dependent on a solid foundation of number knowledge.

The impact of domain-general skills also reduces in comparison to domain-specific skills (i.e. maths-related skills) as students progress in their schooling. Working memory — and in particular, spatial abilities — while predictive of maths success in the early years, have less impact in later primary school. [131] This means prior knowledge in mathematics becomes increasingly important as the demands of the maths curriculum increase. However, cognitive traits continue to play a role in the rate of mathematical learning throughout primary school.[132] [133]

Different number ranges and representations are predictive at different times

While all three subdomains of number sense are significant across the early years of development, research has demonstrated there is a developmental sequence in which children are able to apply knowledge in these domains — both with respect to number range and representation.[134] In the preschool years, children’s number sense is initially heavily influenced by working with non-symbolic representations of quantities within their subitising range (1-4). Because children are able to understand the cardinality (how many) of these sets through subitising, they are capable of demonstrating knowledge with number relations and simple operations with concrete materials in this range prior to extrapolating that knowledge to progressively larger sets.

At the Foundation and Year 1 levels, facility with symbolic number in these domains becomes increasingly important in predicting future success. Hence, screeners feature an increasing weighting towards tasks with numerals as students progress through school. In addition, predictive tasks reflect a progressive increase in the number range to which students can apply their number sense (specifically number and number relations subdomains); from numbers to 20 in Foundation, to 100 in Year 1.

Different skills/competencies are predictive of short-term vs longer term achievement

Research has revealed different aspects of number competence measured in the early years predict short- versus long-term achievement. More intuitive number skills — such as the Approximate Number System (ANS), measured by comparing two significantly different quantities of dots — are more predictive of maths achievement in the early years of schooling. In contrast, success in later primary school is more dependent on arithmetic knowledge such as calculations and using arithmetical operations.[135]  The implication is that while intuitive skills lay the groundwork for initial learning about number, they are insufficient for longer-term success with school mathematics which relies more on facility with precise arithmetic.

Therefore, screening assessments at different year levels should be customised to the stage of schooling; measures should focus on skills that are both most predictive but also most relevant to educational decision making at that stage.

Fluency is more sensitive than accuracy

Having established what to measure, we then need to consider how. Is it enough to be accurate with skills, or do children also need to be fluent, in order to succeed in later mathematics? How do we ensure we are measuring these skills efficiently, in ways that lead to accurate decisions about who is at-risk?

Most research studies which have confirmed the utility of early maths screening measures have used timed delivery, collecting data about the rate of correct responding. Some researchers have investigated the relative value of children’s accuracy in responding to these tasks as opposed to their fluency. Fluency research has a long history in education and refers to the efficiency and flexibility with which children can access information that has been learned and find solutions to problems. In mathematics assessment, fluency is most often measured through timed tasks that give a value of how many correct responses have been given in a set timeframe. If children respond more quickly, it is assumed they are therefore using more efficient strategies that demand fewer mental resources.

In timed testing, it is possible for students with the same score to have different profiles of responses. For example, one student might be slow but accurate while another student with the same score responds quickly but makes a large number of errors. Adding an accuracy criterion to the decision making formula would distinguish between these two profiles.

Amanda VanDerHeyden and colleagues recently reviewed the evidence about the value of accuracy and fluency criteria in decision making.[136] Adding an accuracy criterion (percentage correct responses) to the fluency criterion added nothing to the accuracy of screening measures in mathematics. Students who were fast tended to be accurate, and those who were inaccurate tended to be dysfluent. Therefore, students who were dysfluent were at risk.[137] A more detailed diagnostic assessment could then be administered to shed light on the particular strategies and patterns of error being shown by individual children identified as dysfluent, to inform support.

Measuring fluency makes sense as research shows the slow speed of processing numerical information and executing numerical procedures is a hallmark of children with mathematical difficulties (MD). Students with MD are slower to make numerical comparisons (which number is bigger/more)[138] and tend to use slower and more effortful counting procedures for a longer period of time — not switching to retrieval from memory.[139]

Fluency also has the added benefit of being sensitive to changes over time. When measuring accuracy alone, children may reach 100% accuracy in responding, at which point no further growth can be measured. This is known as a ‘ceiling effect’. The highly accurate student may still be very slow and effortful in completing the maths task, which will reduce both their ability to apply that skill in other contexts effectively, and their likelihood of retaining that skill over time.

In contrast, a fluency measure continues to show growth after students have acquired skills (achieved accuracy) and are becoming more efficient in applying them (increasing fluency). This means well-designed screening tools can be used or adapted to measure students’ progress over time and inform decisions about whether students are responding sufficiently to instruction, or whether a change needs to be made.

How well do current tools fit criteria as screening measures?

It has been established that effective screening tools have the following characteristics:

• They yield reliable scores
• They generate scores that predict future mathematics difficulty
• Their scores lead to accurate decisions and have sensitivity (don’t miss children at-risk) and specificity (don’t identify children who would catch up anyway). Ideally, screening measures should have the capacity to be repeated or triangulated with other tools to make identification more accurate (gated screening).
• They are easy and efficient to administer (in both time and money)
• They have clear decision rules (classify children as ‘at risk’ and ‘not at-risk’) and have direct implications for instruction

The conceptualisation of a multi-tiered approach to support which encompasses universal screening measures is fairly new to the education landscape in Australia. Therefore, the mathematics assessment tools currently in use in Australia were not designed with the specific intention of screening children for mathematical difficulties – therefore to map them against the criteria for such tools may be considered unfair. However, as they are the dominant tools available to schools for early maths assessment purposes, it is useful to consider to what extent they meet the need for screening.

Are they reliable?

Herbert Ginsburg, a leading researcher in understanding children’s thinking about mathematics, described it this way: [140]

“At the heart of the clinical interview method is a particular kind of flexibility involving the interviewer as measuring instrument. Although usually beginning with some standard problems, often involving concrete objects, the interviewer, observing carefully and interpreting what is observed, has the freedom to alter tasks to promote the child’s understanding and probe his or her reactions; the interviewer is permitted to devise new problems, on the spot, in order to test hypotheses; the interviewer attempts to uncover the thought and concepts underlying the child’s verbalizations. The clinical interview seems to provide rich data that could not be obtained by other means.”

Fundamental to a successful interview is a skilled and well-informed practitioner who can interpret and respond to children’s thinking in real time to gain an accurate picture of their current thinking strategies and misconceptions. This knowledge then enables the educator to give appropriate feedback and support.[141]

On the other hand, a poorly administered diagnostic interview can, at best, give unreliable results; and at worst, distort children’s thinking.[142]  Therefore, it is unsurprising that the clinical interview method has become central to research projects intending to develop teacher knowledge about the learning and teaching of mathematics, termed ‘pedagogical content knowledge’. The utility of individual interviews in concert with professional learning for developing teacher knowledge is well established in maths education literature.[143] [144] [145]

Approaches that incorporate the use of individual interviews, such as the Early Numeracy Research Project and Mathematics Recovery, have also recognised the need for significant professional development to ensure teachers are able to use and interpret the interview tools successfully. Such training requires a further investment, which is rarely funded by school systems.

In sum, individual diagnostic interviews can be reliable measures of students’ mathematics abilities, but this is very much dependent on the expertise of the interviewer.

Do they have sufficient predictive validity? Sensitivity and specificity?

Measures that produce scores with good predictive validity are good predictors of later maths achievement. Central to this idea is, of course, the collection of data mid-stream while the opportunity still exists for intervention to be delivered. As stated earlier in this paper, the design of standardised achievement tests as infrequent measures typically administered at the conclusion of an instructional period (e.g. to inform end-of-year reporting) is at odds with the purpose of a screener as ‘predictive’.

Having ‘predictive validity’ may mean the test scores themselves have been shown to predict later maths achievement, or mastery of the skills measured is predictive of later achievement.

According to the research described earlier in this paper, such tools should measure the construct of ‘number sense’: number (including counting), number relations and number operations (including addition and subtraction combinations). However, the complexity of skills within those domains, and the relative value of them, changes as students gain proficiency in maths.[146] Screening measures focused on number knowledge and number relations have a higher predictive validity in the Foundation Year, whereas operations and calculation gain importance in Year 1. Measurement under timed conditions is valuable to indicate fluency.

A number of the tools in use in Australian schools do measure aspects of number sense, particularly interviews.

Both interviews and standardised assessments typically collect information across a range of mathematical areas. While many of the interview tools focus on early number skills and number sense, most also gather information across multiple domains of mathematical knowledge including time, measurement and shape (see Table 2).

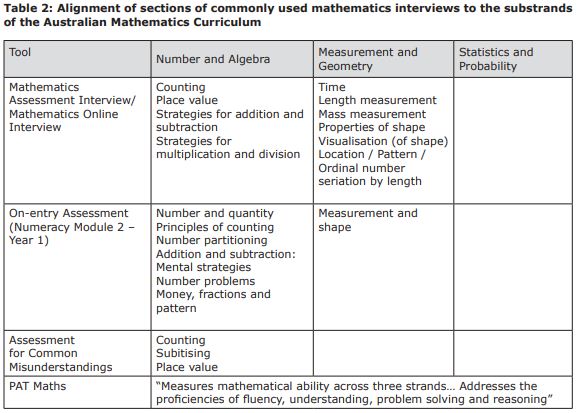
Within the domain of number, current interviews sample some of the skills and knowledge shown to predict mathematical achievement. These include counting, number recognition and addition/subtraction strategies (see Table 3).

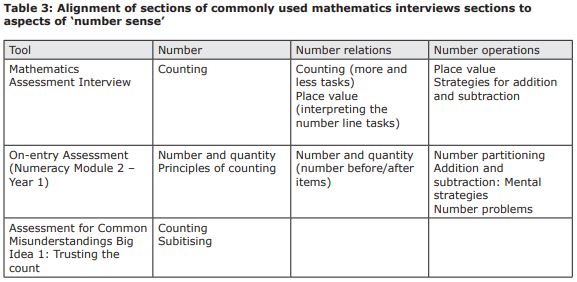
Table 2 shows that both the MAI/MOI and On-entry Assessment (Numeracy Module 2) measure skills related to number sense, while the Assessment for Common Misunderstandings measures a subset of these. While the testing of number sequence is fairly common, only the MAI also includes an item targeting number magnitude (plotting a number on a bounded number line), which has been shown to be related to future success with mathematics.

Due to the interview format, none of the tasks in these tools are presented in ways that could measure fluency, which has been identified as a key difference between students with and without mathematical difficulties. Many also include geometry and measurement items that — although undoubtedly useful for teaching — have not been shown to be predictive of future achievement in mathematics.

The Progressive Achievement Tests, when administered at the beginning of high school, have been shown to predict mathematics grades later in high school.[147] Such studies have not been conducted in primary school. The scope of the PAT-Maths is not focused on number sense and samples across all content and proficiency strands, as might be expected of a test primarily designed to measure achievement (rather than risk).

Tools designed for screening assist educators to make decisions about who is at-risk and needs additional support.  The tools currently in use in Australian schools were not designed for this purpose, but to gather diagnostic information about children’s current strategies and knowledge (interviews) and maths achievement (standardised achievement tests). While they do include tasks that can reasonably be expected to predict maths achievement, most do not attempt to classify children as at-risk/not at-risk. Those that do have not been studied in ways that enable analysis of decision accuracy.

Despite this limitation, existing tools could still inform an effective screening process if used strategically. In an Australian context where systematic screening processes are still being established, an acceptable second ‘gate’ may be to use existing mathematics assessment tools with students identified as at-risk by the universal screener focused on number sense. Using existing tools in this way would satisfy a core underlying principle of gated approaches to screening: to triangulate data from multiple sources. In this model, such tools would require decision rules so teachers could clearly identify who was at-risk according to the second gate. This process could both increase decision accuracy and reduce the number of students needing more time-intensive assessment methods.

Are they efficient?

According to internationally renowned mathematics and reading instruction expert Dr Russell Gersten,[148] “we understand a good deal more about what comprises a comprehensive assessment battery, but are less certain of the elements of an efficient assessment battery” (p.441). The comprehensive nature of the maths assessment techniques currently in use in Australia and outlined above are a reflection of this challenge.

Using individual interviews to determine mathematical strategies has practical disadvantages. For one, the considerable investment of time (and therefore money). The individual interviews commonly used for early mathematics assessment in Australia take at least 30 minutes per student to administer. Across a class of 24 children, this translates to a loss of around 12-16 instructional hours, at a cost of around $1300-$1600 per classroom (relief teacher cost only). Further time is then required to interpret the interview results and incorporate the implications into classroom planning.

Standardised achievement tests are undoubtedly more efficient to administer, typically requiring a single classroom period. However, further time is then required to train teachers to analyse and interpret results, and then enable them to do so, so that data gathered can be applied to classroom planning.

Do current tools have clear decision rules that lead to instructional actions?

Interview tools differ in the extent to which they supply decision rules. In some systems, a criterion of minimum ‘growth points’ on the MAI is used to determine which children are at risk. If an intervention program (e.g. Extending Mathematical Understanding [EMU]) is offered at that school, students are then recommended for inclusion. In contrast, teachers from WA receive a spreadsheet of On-entry Assessment results without specific guidance on how the information should be used to identify at-risk students or provide support. These decisions are left to the discretion of and are dependent on the expertise and resources of the teacher.

Similarly, standardised achievement tests provide standardised scores that rank students against the scores expected of their age peers. Teachers can broadly see which students are performing above, below and at average levels for their age. Some guidance may be provided as to the sorts of skills that typically benefit students at particular levels of achievement. However, due to the large amount of information provided across such a broad range of concepts and skills, it can be challenging for teachers to know where to start in responding to this data, and no ‘decision rules’ are provided.

Effective screening tools must not only identify who is at risk, but specify an appropriate educational response. In addition to accurately predicting mathematics difficulty, ‘number sense’ is a useful construct for teachers because the skills and knowledge it comprises are teachable and lead to direct implications for classroom teaching and intervention programs. The components of ‘number sense’ that predict mathematics achievement in formal schooling are not those we would consider ‘biologically primary’ (or innate) skills. Knowing the sequence of counting words, counting collections observing the principles of counting, representing collections with numerals and representing/comparing the magnitude of numerals are ‘biologically secondary’ skills which require instruction, as are solving mathematical number problems and completing precise calculations.

Although such learning is usually ‘playful’, children do not learn the skills listed above in societies without formal educational systems. Even where children enter formal schooling already having some of those skills, it is due to the presence of some sort of explicit informal instruction in the home which resembles experiences provided in school settings.[149]

Therefore, screening that targets aspects of ‘number sense’ as defined in this paper fulfils the requirement to inform instructional actions. There are numerous examples of interventions focused on number sense that have led to significant, sustained improvements in achievement.[150] [151] [152] [153]

Are current tools fit for screening purposes?

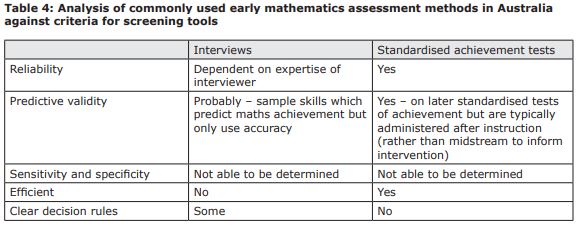
Analysis reveals that the current tools in use have the capacity to yield reliable information and may produce scores with predictive validity. Most do not have clear decision rules and are highly inefficient (refer to Table 4).

There is no question that talking to students about their mathematical strategies reveals important information for teaching. Such conversations could be considered essential to inform educational interventions for those students who are not benefiting from high quality teaching in the classroom and for whom existing instructional adjustments are not working.  Individual interviews come at considerable cost, both in monetary terms and in instructional time. For students working at grade-appropriate levels, this investment may have minimal — if any — impact on the instruction they subsequently receive.

Individual interview tools have demonstrated utility for teacher professional development and to gain insight into the strategies and misconceptions of students for whom more targeted teaching is needed (e.g. as used in Math Recovery and Extending Mathematical Understanding [EMU] Programs). Their utility for diagnostic purposes, particularly with students with limited reading skills, is well established and justifies the large investment of time. However, by their very design, universal screening tools are quick and efficient to deliver to entire classes to minimise the loss of instructional time and maximise the impact of more targeted instruction. Therefore a more judicious use of interview-based tasks is required than is currently the norm in Australian schools.

Standardised tests of mathematics achievement (e.g. PAT Maths) provide essential data about the effect of instruction on general mathematics achievement and whether children are ‘on track’ with grade-level norms. For students receiving intervention, they are very useful as infrequent pre-and post-tests to determine if children are ‘catching up’ to their peers and to support further decision-making.

Screening measures administered to all students should focus on those skills most foundational to — and therefore most predictive of — future achievement in maths, so more intensive diagnostic efforts and intervention can be targeted to where they are needed. Australian teachers and schools need access to specific tools designed for this purpose.

The role of general educational risk factors

Although general educational risk factors matter, these are not suited to universal screening purposes. Research has revealed that a number of aspects of ‘general intelligence’ also have strong relationships with, and are predictive of, maths achievement in the early years. Better working memory capacity,[154] [155] [156] [157] attention,[158] spatial skills[159] and fluid reasoning[160] are associated with higher maths achievement. Some studies have also suggested strong general cognitive skills are associated with faster mathematical progress.[161] For explanations of the general cognitive skills most commonly associated with maths achievement, see Box 6.

Early spatial skills have been found to predict maths achievement as early as age three. However, it is unclear whether growth in spatial skills impacts on maths achievement. While early spatial skills seem to be important, one study found no relationship between improvement in spatial skills and rate of maths learning. [163] Conversely, a recent study of 17,000 six- to eight-year-olds appeared to show a positive impact on arithmetic from training spatial skills, particularly spatial pattern completion and spatial memory (such as remembering the sequence of dots touched on an array).[164]

Other studies show the impact of spatial skills on general mathematics achievement might be largely due to the brain’s spatial representation of the number line.[165] In the latter case, it would be more impactful to target teaching efforts towards concepts about number value rather than general spatial skills.

Rapid Automatised Naming (RAN) has also been found to be associated with higher maths achievement, in particular, better mathematical fluency (calculation).[166] RAN is thought to be a measure of the speed of retrieving information from long-term memory, but may also measure speed at processing written symbols. Both of these are required to recognise and respond to arithmetic tasks. Poor RAN has been found to be associated with very poor rates of mathematical learning in the first five years of school.[167]

It has therefore been suggested that some of these skills should feature in early maths screeners. However, measuring and subsequently targeting cognitive skills presents challenges. Tasks to measure aspects of general intelligence are normally featured in cognitive assessment batteries delivered one-to-one by psychologists and rarely feature in assessments designed for teacher administration. Another issue is that although such weaknesses may increase risk, the evidence regarding whether training domain-general skills transfers to academic skills is mixed. Certainly, the impact on mathematical skills is greater from instruction directly targeting those skills.

It is questionable whether measuring skills that cannot be impacted through classroom instruction adds value to screening processes. These traits are associated with higher levels of risk for mathematical difficulties, but this risk is measurable in other ways better suited to educational contexts (i.e. measuring maths-related skills). Therefore, it seems unlikely that time testing cognitive abilities would currently be well spent at the screening stage. Further research may demonstrate the impact of training on maths learning more definitively, and  reveal practical ways this can be achieved in classrooms.

Socioeconomic status is also a risk factor for poor mathematics achievement,[168] which is outside the influence of school systems. Children from disadvantaged backgrounds tend to begin school with significantly lower levels of existing mathematical skills and knowledge, especially related to verbal aspects of mathematics such as knowing the meaning of number words and interpreting verbally presented number problems.[169] [170] This makes sense in light of research showing language ability, and in particular mathematical vocabulary, is correlated with and predicts mathematical achievement.[171] [172] [173]

Stable traits such as low socioeconomic status, and apparent difficulties with memory and/or attention could merit a higher threshold for determining risk. That is to say, it would be wise for a child only slightly above an at-risk cut-off but who possessed other risk factors to be monitored more carefully than other children deemed not at-risk.

Implications for policy and practice

The federal government’s Year 1 Number Check is insufficient to meet screening needs

The online Year 1 Number Check has some of the required features of an effective screener. However, the brief form is likely to lack sensitivity and underestimate the number of students requiring support. In order to effectively predict Year 1 achievement, it requires a stronger focus on number operations and the ability to measure fluency with arithmetic combinations. Further attention to the domain of ‘number relations’ — and in particular, number magnitude (as measured by plotting numbers accurately on a bounded number line) — is also needed given the significance of the development of a ‘mental number line’ as discussed earlier in this report.

If the Year 1 Number Check is to be used as an effective screener, following these content changes it should be the subject of research to determine appropriate decision rules. Any ‘cut scores’ should be validated by research predicting future achievement (in keeping with the purpose of a screener) and not solely mapped to curriculum expectations.

Identification of struggling students must be more efficient and systematic

The recent report of the Better and Fairer Review recognised the value of Multi-Tiered Support Systems (MTSS) to improve educational outcomes for Australian children. MTSS are multi-layered prevention and intervention systems which include specialised assessment practices at each level.

At Tier 1, in the context of this report, an MTSS framework includes effective screening processes to identify students at risk of maths failure. For efficiency and to assist decision making about instructional support, such measures should target only those areas relevant for assessing risk. This would also help to direct more time-intensive diagnostic measures to where they are most needed and maximise time spent teaching and learning.

Many of the current interviews used in Australian schools fit this description as primarily ‘diagnostic.’ As such, they are better suited to higher tiers of MTSS assessment. Due to their individualisation and detail, individual interviews can be used to get to the root of these difficulties and identify errors, strategies or misconceptions that can then be the target of intervention efforts.[174]

Alongside screening, teachers and schools should be supported to continue with their existing practices of collecting data on student learning needs and achievement through a variety of methods as part of high quality teaching. Data to inform the planning of teaching and learning cycles should be gathered as it is needed for instruction.

Teachers need manageable ways of, and tools for, intensifying instruction

To increase the accuracy of screening tools and intervention decisions, a gated screening approach is advantageous. Gated screening requires a re-administration of screening or some form of careful progress monitoring after a period of increased instructional intensity.

Increasing instructional intensity can increase academic outcomes for students and gives children identified as at-risk extra opportunities to benefit from instruction.[175] [176] Increasing intensity can be achieved through a number of techniques, including: making greater use of evidence-based practices, explicitly teaching children how to transfer their skills to novel contexts, and including instruction in self-regulation strategies (e.g. self-monitoring skills) as additional components of high quality maths instruction.[177] Other intensification techniques require extra resources such as decreasing group size or increasing the duration or frequency of instruction. [178]

One technique for increasing intensity that does not require additional resourcing is increasing students’ opportunities to respond and receive corrective or affirmative feedback.[179] Well-designed explicit instructional approaches plan for frequent student responses (as often as every 30 to 60 seconds) through choral responses, gestures, written whiteboard responses and brief, carefully structured peer interactions.

Classwide intervention models, like Peer-Assisted Learning Strategies (PALS) and SpringMath, provide another effective way to intensify instruction.[180] Specially designed pairings of students work together on using highly structured peer tutoring routines to build fluency with core skills.

Teachers and schools need access to this knowledge so that they can better support struggling students using the resources available to them.

Screen and monitor progress in the three domains of ‘number sense’ at least twice yearly

Early screening and intervention are crucial. Screening should focus on the skills most crucial to, and most predictive of, future success in mathematics.

Screening tools are different from diagnostic tools. Screening should be conducted with all students at least two times per year; once in mid-term 1, and once at the beginning of term 3. At the end of the year (mid-term 4), existing standardised tests of achievement can be used as a means of program evaluation and to offer additional data for formal reporting.

When students are identified as ‘at-risk,’ progress should be carefully monitored as instructional intensity is increased. Students who do not progress at expected rates due to this increase should then be the subject of more diagnostic assessment to find out the source of their difficulties. Current interview tools could be suited to this purpose. These students should then receive ‘tier 2’ interventions in addition to their core mathematics instruction in ‘tier 1,’ consistent with the MTSS model.

Diagnostic assessment remains an important tool for teachers to inform classroom teaching. In addition to using individualised tools with students at risk, teachers should continue to collect diagnostic data to inform their teaching, e.g. to ascertain prior knowledge of the class on place value immediately before commencing teaching related to place value.

An early focus on building maths knowledge should include all three components of early ‘number sense’

Foundation and Year 1 classes should include instruction and daily practice to build knowledge and fluency with aspects of ‘number sense’. The early years of schooling need to focus on building a connected body of knowledge about small numbers including their representation (symbols, objects and drawings), sequence, value (magnitude), composition (number facts and early place value) and operations (addition and subtraction). It is important that children consolidate and then move beyond counting from one to combine collections. As children move into Year 1 they need to extend this knowledge to a greater focus on operations, involving adding to, removing from, combining and separating sets (addition and subtraction), and moving to memory based strategies for small number combinations (fact retrieval).

Fluency with that body of knowledge is important. Students need daily practice in core number skills so working memory can be available to apply those skills and knowledge in different contexts. Daily practice should focus on grade-appropriate number ranges including number recognition, reciting the counting sequence forwards and backwards from different starting points, sequencing numbers and decomposing and composing numbers (e.g. breaking 9 into 4 and 5 or 14 into its place value components of 10 and 4).

From Year 1, students need to be supported to start building a bank of known addition and subtraction facts.  This knowledge should be built up methodically, i.e. starting with ‘count on’ strategies, progressing to number combinations (e.g. doubles, combinations of ten) and teaching students to use known facts to quickly derive other facts (e.g. if 6 + 4 = 10 then 6 + 5 = 11). Students should be taught the relationship between addition and subtraction so that they recognise that they can use knowledge of addition to solve subtraction, i.e. seeing 10 – 6 as 6 + _ = 10. Regular practice should have the goal of moving students to fluent performance, where most facts are ‘known’ and do not require the use of strategies but are retrieved from memory.

A research-validated, nationally-consistent screening tool should be implemented in Year 1

Well-designed screening tools can identify children likely to struggle with numeracy earlier than Year 1. Policymakers should support adaptation of internationally validated screening tools for Year 1, as well as the potential for earlier years including Foundation level (equivalent) to the Australian context in addition to Year 1. While systematic screening at this level is not an initial priority, guidance for preschool educators should focus on building number and number relations skills initially within the subitising range (1-4), and then up to 10.

To enable such research to occur and build a more evidence-based culture in Australian schools, policymakers should streamline the process by which research can be conducted in Australian schools with Australian students. Protracted, complicated processes for such research discourage the systematic testing of screening and intervention tools. Researching the impact of such tools and programs could provide essential data to improve the educational outcomes of students.

Screening tools designed for Foundation and Year 1 levels should measure the acquisition of aspects of ‘number sense’. The complexity and balance of these domains should vary between Foundation and Year 1. Foundation screening should concentrate more on number knowledge, number relations and early operations knowledge. Year 1 screening should have a heavier focus on number relations, operations, efficient counting and solving addition and subtraction problems.

In addition to subdomain weighting, these tools should reflect research on the children’s development in both number range and form of representation. In the domains of number and number relations, Foundation tasks should feature numbers to 20 and Year 1 to 100. In the domain of number operations, Foundation tasks should focus on combinations within 10 and Year 1 up to 20. Foundation screeners should feature a mix of symbolic and non-symbolic tasks (e.g. involving objects or representations), particularly for number operations tasks, whereas Year 1 screeners should have a greater focus on symbolic representation.

Screening tools must be efficient. In Year 1, group-administered, timed tasks which measure fluency with key predictive skills should be a core feature, with a limited number of skills assessed through interview to appropriately balance the need for detail and efficiency. In Foundation this balance will differ, with a relatively greater proportion of tasks delivered through interview.

Screening should be implemented within a broader systemic approach to support (MTSS), where clear processes exist around progressively intensifying instruction for at-risk students based on data, and regularly monitoring progress. While two screening periods per year are recommended for ‘universal screening’ as outlined above, the middle screening period should be nationally consistent and involve the national collection of data. This data should be used to track the health of the education system over time and available to individual schools to support educational planning and provision. It is not recommended that school level data be published publicly (i.e. as for NAPLAN).

The screening tool should therefore be designed and researched to provide accurate data about risk status at both time-points. This means once a screening tool is chosen or developed, it should be the subject of research in the Australian context to develop accurate cut-off scores (decision rules) that indicate risk at each time period.

Systems should realign existing assessment tools for a multi-tiered framework

Screening and intervention tools must streamline and target the work of teachers rather than adding to it. Existing assessment tools administered with whole cohorts of students should be reconsidered and aligned to their appropriate purpose and tier within an MTSS framework. Teachers should reserve more detailed diagnostic assessment (e.g. extended individual interview tools) for students identified through initial screening processes.

Evidence-based professional development could assist teachers to better interpret and act on screening data

Teachers and schools should have access to evidence-based professional development and resources to assist them to intensify instruction. Such intensification can make use of the variety of strategies outlined in the Taxonomy of Intervention Intensity[181] and guidance from the Center on Multi-tiered Systems of Support.[182] A focus on increasing opportunities to respond and receive feedback (which does not necessitate more personnel) should be central. Professional learning and guidance should also be provided to assist in monitoring the progress of students identified as ‘at-risk’. This will then increase decision accuracy for the allocation of more intensive, small group instruction.

To inform the development of such professional learning, research should be conducted in the Australian context on the application of specific instructional techniques to increase opportunities to respond. The Australian Education and Research Organisation (AERO) could be commissioned to research and develop resources and guidance to support the use of such techniques including classwide intervention.

Screening and intervention tools must generate scores that are reliable, valid and useful for teaching. Screening tools should be accompanied by clear guidance and resources to support teachers to act on the data collected.

Intervention programs and resources are needed

Teachers and schools need access to systematic evidence-based programs to target identified difficulties in number sense and the resources with which to deliver those programs. As previously identified in this report, well-designed interventions targeting number sense have demonstrated significant impacts on children’s achievement when implemented with fidelity. Australian schools and teachers need access to such programs.

Given current workforce challenges, highly structured, ideally scripted programs would be most suitable for this purpose. This would help ensure programs are delivered with fidelity regardless of the deliverer’s level of qualification and experience.

Progress monitoring tools are needed

There are multiple opportunities to use curriculum-based measures for monitoring and influencing achievement, as identified by research.[183] Only one has been explored deeply in this report: the use of single-point-in-time measures to predict achievement and target support. Measures to monitor growth over time are necessary to monitor the effectiveness of instructional programs and interventions.[184] This is especially important given that although well-designed mathematical interventions can be very effective, students who struggle with mathematics may have particular cognitive weaknesses such as difficulties with executive function which put them at high risk of falling behind again if support is not maintained.[185]

This need for a longer-term, systematic approach is reflected in the fact that mathematics interventions can be subject to significant fade-out effects; hence providing intervention is not a ‘set and forget’ solution. Early intervention is necessary but insufficient to close the gap in achievement in the long term. [186] Students who effectively ‘catch up’ to their peers in the early years through effective intervention may retain their skills but not necessarily maintain the pace of learning required in the regular classroom without support.

Screening and intervention must be ongoing

Screening for difficulties, providing intervention and monitoring progress through those interventions can be expected to occur repeatedly in cycles throughout schooling for some students. As the demands of the mathematics curriculum change, for example from a focus on whole number arithmetic in the early primary years to fractions and decimals in the middle and upper primary years, students who were not at-risk on foundational skills may begin to experience skill gaps.[187] Therefore, mathematics screening should continue as part of a well-implemented MTSS through Year 8 reflecting beginning algebra skills.[188]

Future system priorities should include considering which tools can assist teachers to effectively and efficiently monitor the mathematical growth of students throughout their schooling, and intensify instruction as needed to ensure these students can maintain pace with grade level expectations. Universal screening processes should be considered necessary throughout schooling, particularly concerning later ‘gateway skills’ such as multiplicative and fractional knowledge, which are known to be highly predictive of success with later mathematics.[189]

Long term effectiveness requires high quality ‘tier 1’ curriculum and instruction

Another likely reason for ‘intervention fade out’ is the impact of what’s been termed the forgetting curve:[190]

“…if forgetting is steeper for individuals who have acquired more skill, and learning is steeper for individuals with less skill, then skill levels of the more skilled treatment group and the less skilled control group will converge.”

Hence, when intervention concludes and students return to dependence on regular classroom instruction, the quality of that instruction is paramount. If students do not have regular opportunities to retrieve, use and build upon what has been learned in intervention, this will be rapidly lost. The impact of this ‘forgetting curve’ underscores the importance of a systematic approach to improving mathematics achievement through high quality instruction at all three tiers.

Conclusion

This paper has outlined an evidence-based framework for a screening tool for early numeracy difficulties. Unfortunately, the review of present practices suggests that although the schools and teachers are aware of, and value, the need to screen students for numeracy difficulties, they currently lack the tools to do so in efficient and accurate ways. This results in significant financial and instructional cost — to governments, schools and students — of inaccurate and inefficient methods. This in turn has implications for the decisions schools make about intervention. For four in five struggling Year 3 students, these early numeracy difficulties forecast ongoing numeracy struggles throughout Primary and Secondary schooling.[191] The stakes are high for these students and urgent policy solutions are required.

We know a great deal about how to predict who will struggle with mathematics, and what support will give such students the best chance of long-term success. What we lack is a coordinated response for putting this into the hands of schools and teachers in practical and efficacious ways. The Australian education system has a unique opportunity to do so now through the development or adoption of an evidence-based tool to identify children at risk of maths failure in the earliest years of school, and to do so in a way that directly impacts teaching and learning.

Of course, predicting who will fail achieves nothing if we do not then leverage the same research and effort to design a safety net for those students. While a consistent and evidence-based approach to screening is a necessary first step, to have a significant long-term impact on achievement it must sit within a systematic approach that includes progressive intensification of instruction (MTSS). The nation’s children deserve nothing less.

Endnotes

[1] Thomson, S., Wernert, N., Rodrigues, S., & O’Grady, E. (2020). TIMSS 2019 Australia. Volume I: Student performance. Australian Council for Educational Research. https://doi.org/10.37517/978-1-74286-614-7

[2] OECD (2023). PISA 2022: Factsheets Australia. https://www.oecd.org/publication/pisa-2022-results/country-notes/australia-e9346d47/

[3] OECD (2023), Education at a Glance 2023: OECD Indicators, OECD Publishing, Paris, https://doi.org/10.1787/e13bef63-en.

[4] Aunola, K., Leskinen, E., Lerkkanen, M.-K., & Nurmi, J.-E. (2004). Developmental Dynamics of Math Performance From Preschool to Grade 2. Journal of Educational Psychology, 96(4), 699–713. https://doi.org/10.1037/0022-0663.96.4.699

[5] Claessens, A., & Engel, M. (2013). How Important Is Where You Start? Early Mathematics Knowledge and Later School Success. Teachers College Record (1970), 115(6), 1–29. https://doi.org/10.1177/016146811311500603

[6] Jordan, N. C., Kaplan, D., Oláh, L. N., & Locuniak, M. N. (2006). Number Sense Growth in Kindergarten: A Longitudinal Investigation of Children at Risk for Mathematics Difficulties. Child Development, 77(1), 153-175. https://doi.org/10.1111/j.1467-8624.2006.00862.x

[7] Jordan, N. C., & Levine, S. C. (2009). Socioeconomic variation, number competence, and mathematics learning difficulties in young children. Developmental Disabilities Research Reviews, 15(1), 60–68. https://doi.org/10.1002/ddrr.46

[8] Garon-Carrier, G., Boivin, M., Lemelin, J.-P., Kovas, Y., Parent, S., Séguin, J. R., Vitaro, F., Tremblay, R. E., & Dionne, G. (2018). Early developmental trajectories of number knowledge and math achievement from 4 to 10 years: Low-persistent profile and early-life predictors. Journal of School Psychology, 68, 84–98. https://doi.org/10.1016/j.jsp.2018.02.004

[9] Davis‐Kean, P. E., Domina, T., Kuhfeld, M., Ellis, A., & Gershoff, E. T. (2022). It matters how you start: Early numeracy mastery predicts high school math course‐taking and college attendance. Infant and Child Development, 31(2).

[10] Koon, S., & Davis, M. (2019). Math Course Sequences in Grades 6-11 and Math Achievement in Mississippi. REL 2019-007. In Regional Educational Laboratory Southeast. Regional Educational Laboratory Southeast.

[11] Bynner, J., & Parsons, S. (2001). Qualifications, Basic Skills and Accelerating Social Exclusion. Journal of Education and Work, 14(3), 279–291. https://doi.org/10.1080/13639080120086102

[12] Litster, J. (2013). Impact of poor numeracy on adults. National Research and Development Centre for Adult Literacy and Numeracy.

[13] OECD (2017), OECD Economic Surveys: Australia 2017, OECD Publishing, Paris, https://doi.org/10.1787/eco_surveys-aus-2017-en.

[14] Building Skills for All in Australia: Policy Insights from the Survey of Adult Skills. OECD Skills Studies. (2017). Building Skills for All in Australia: Policy Insights from the Survey of Adult Skills. https://doi.org/10.1787/9789264281110-en

[15] Jackson, C., Wan, W.-Y., Lee, E., Marslen, T., Lu, L., Williams, L., Collier, A., Johnston, K., & Thomas, M. (2023). Which skills are important for future literacy and numeracy learning? How the Australian Early Development Census data reveal the building blocks for future reading, writing and numeracy performance. Australian Education Research Organisation. https://www.edresearch.edu.au/ resources/literacy-numeracy-skills-future-learning

[16] Productivity Commission 2022, Review of the National School Reform Agreement, Study Report, Canberra.

[17] Bailey, D. H., Watts, T. W., Littlefield, A. K., & Geary, D. C. (2014). State and Trait Effects on Individual Differences in Children’s Mathematical Development. Psychological Science, 25(11), 2017–2026. https://doi.org/10.1177/0956797614547539

[18] Clements, D. H., Sarama, J., Layzer, C., & Unlu, F. (2023). Implementation of a Scale-Up Model in Early Childhood: Long-Term Impacts on Mathematics Achievement. Journal for Research in Mathematics Education, 54(1), 64–88. https://doi.org/10.5951/jresematheduc-2020-0245

[19] Clements, D. H., & Sarama, J. (2011). Early childhood mathematics intervention : Investing early in education. Science (American Association for the Advancement of Science), 333(6045), 968–970.

[20] Karoly, L.A., Kilburn, M.R. & Cannon, J.S. (2005). Research Brief: Proven benefits of early childhood interventions. Rand Corporation,

[21] Buckingham, J., Nayton, M., Snow, P., Capp, S., Prince, G., & McNamara, A. (2017). National Year 1 Literacy and Numeracy Check: Expert Advisory Panel: Advice to the Minister. https://www.education.gov.au/quality-schools-package/resources/year-1-check-expert-advisory-panel-final-report

[22] O’Brien, L., Paul, F., Anderson, D., Hunter, J., Lamb, S., & Sahlberg, P. (2023).   Improving Outcomes for All: The Report of the Independent Expert Panel’s Review to Inform a Better and Fairer Education System. https://www.education.gov.au/review-inform-better-and-fairer-education-system/resources/expert-panels-report

[23] CESE (Centre for Education Statistics and Evaluation) (2023). COVID Intensive Learning Support Program – Phase 3 evaluation. NSW Department of Education.

[24] Cueli, M., Areces, D., García, T., Rodríguez, C., Vallejo, G., & González‐Castro, P. (2019). Influence of initial mathematical competencies on the effectiveness of a classroom‐based intervention. British Journal of Educational Psychology, 89(2), 288–306. https://doi.org/10.1111/bjep.12239

[25] Vanderheyden, A. M., & Codding, R. S. (2015). Practical effects of classwide mathematics intervention. School Psychology Review, 44(2), 169-190. https://doi.org/10.17105/spr-13-0087.1

[26] Clements, D. H., Sarama, J., Layzer, C., & Unlu, F. (2023). Implementation of a Scale-Up Model in Early Childhood: Long-Term Impacts on Mathematics Achievement. Journal for Research in Mathematics Education, 54(1), 64–88. https://doi.org/10.5951/jresematheduc-2020-0245

[27] Clements, D. H., Sarama, J., Wolfe, C. B., & Spitler, M. E. (2013). Longitudinal evaluation of a scale-up model for teaching mathematics with trajectories and technologies: Persistence of effects in the third year. American Educational Research Journal, 50, 812–850.

[28]  Koch, I. (Ed) (2019). Choose Maths Gender Report: Mathematics and Gender: Are Attitudes and Anxieties Changing towards Mathematics? Melbourne: Australian Mathematical Sciences Institute.

https://amsi.org.au/wp-content/uploads/2019/07/gender-report-2019.pdf

[29] quote from p. 1 of Geary, D.C. (2023). Facing up to maths anxiety: How it affects achievement and what can be done about it. Analysis Paper 61. Centre for Independent Studies.

[30] Koch, I. (Ed) (2019). Choose Maths Gender Report: Mathematics and Gender: Are Attitudes and Anxieties Changing towards Mathematics? Melbourne: Australian Mathematical Sciences Institute.

https://amsi.org.au/wp-content/uploads/2019/07/gender-report-2019.pdf

[31] Ng, C. (2021). Mathematics self-schema, motivation, and subject choice intention: A multiphase investigation. Journal of Educational Psychology, 113(6), 1143-1163. https://doi.org/10.1037/edu0000629

[32] Sheldrake, R., Mujtaba, T. and Reiss, M.J. (2015), Students’ intentions to study non-compulsory mathematics: the importance of how good you think you are. British Education Research Journal, 41: 462-488.  https://doi.org/10.1002/berj.3150

[33] Harari, R. R., Vukovic, R. K., & Bailey, S. P. (2013). Mathematics Anxiety in Young Children: An Exploratory Study. The Journal of Experimental Education, 81(4), 538–555. https://doi.org/10.1080/00220973.2012.727888

[34] Sorvo, R., Koponen, T., Viholainen, H., Aro, T., Räikkönen, E., Peura, P., Dowker, A., & Aro, M. (2017). Math anxiety and its relationship with basic arithmetic skills among primary school children. British Journal of Educational Psychology, 87(3), 309–327. https://doi.org/10.1111/bjep.12151

[35] Buckingham, J., Nayton, M., Snow, P., Capp, S., Prince, G., McNamara, A. (2017). National Year 1 Literacy and Numeracy Check. Expert Advisory Panel: Advice to the Minister. https://apo.org.au/sites/default/files/resource-files/2017-09/apo-nid107126_1.pdf

[36] Devlin, B. L., Jordan, N. C., & Klein, A. (2022). Predicting mathematics achievement from subdomains of early number competence: Differences by grade and achievement level. Journal of Experimental Child Psychology, 217, 105354–105354. https://doi.org/10.1016/j.jecp.2021.105354

[37] Quoted on p.30 in Ginsburg, H. (1997). Entering the Child’s Mind: The clinical interview in psychological research and practice. Cambridge University Press.

[38] Gelman, Rochel., & Gallistel, C. R. (1978). The Child’s Understanding of Number. Harvard University Press. https://doi.org/10.4159/9780674037533

[39] Wright, R. J., Martland, J., & Stafford, A. K. (2006). The Learning Framework in Number. In Early Numeracy. SAGE Publications, Limited.

[40] Smith, T. M., Cobb, P., Farran, D. C., Cordray, D. S., & Munter, C. (2013). Evaluating Math Recovery: Assessing the causal impact of a diagnostic tutoring program on student achievement. American Educational Research Journal, 50(2), 397-428.

[41] Pearn, C. (1999). Empowering Classroom Teachers for the 21st Century: meeting the challenge of advancing children’s mathematical development1. European Journal of Teacher Education, 22(2–3), 277–294. https://doi.org/10.1080/0261976899020277

[42] Higgin, J., & Bonne, L. (2008). The role of the diagnostic interview in the Numeracy Development Projects. https://nzmaths.co.nz/findings-nz-numeracy-development-projects-2008

[43] Bobis, J. (2009). The Learning Framework in Number and its impact on teacher knowledge and pedagogy. NSW Department of Education and Training.

[44] Gervasoni, A., Clarke, D., Clarke, B., Cheeseman, J., Sullivan, P.,  McDonough, A., Horne, M. & Rowley, G. (2002). Early Numeracy Project Final Report.

[45] Gervasoni, A., Roche, A., & Downton, A. (2021). Differentiating Instruction for Students Who Fail to Thrive in Mathematics: The Impact of a Constructivist-Based Intervention Approach. Mathematics Teacher Education & Development, 23(3), 207-.

[46] Department of Education Employment and Training (2001). Early numeracy interview booklet. Department of Education, Employment and Training.

[47] Australian Catholic University. (2011). Mathematics Assessment Interview. Australian Catholic University.

[48] ACER (2024). PAT Assessments. https://www.acer.org/au/pat/assessments

[49] Graham, L. J. (2016). Reconceptualising inclusion as participation: Neoliberal buckpassing or strategic by-passing? Discourse: Studies in the Cultural Politics of Education, 37(4), 563-581. https://doi.org/10.1080/01596306.2015.1073021

[50] Hardy, I. (2014). A logic of appropriation: Enacting national testing (NAPLAN) in Australia. Journal of Education Policy, 29(1), 1-18. https://doi.org/10.1080/02680939.2013.782425

[51] Penn, S. (2023). Uses and abuses of standardised testing: Perceptions from high-performing, socially disadvantaged schools. Issues in Educational Research, 33(1), 266–283.

[52] O’Brien, L., Paul, F., Anderson, D., Hunter, J., Lamb, S., & Sahlberg, P. (2023).   Improving Outcomes for All: The Report of the Independent Expert Panel’s Review to Inform a Better and Fairer Education System. https://www.education.gov.au/review-inform-better-and-fairer-education-system/resources/expert-panels-report

[53] Gersten, R., Beckmann, S., Clarke, B., Foegen, A., Marsh, L., Star, J. R., & Witzel, B. (2009). Assisting students struggling with mathematics: Response to Intervention (RtI) for elementary and middle schools (NCEE 2009-4060). Washington, DC: National Center for Education Evaluation and Regional Assistance, Institute of Education Sciences, U.S. Department of Education. Retrieved from http://ies. ed.gov/ncee/wwc/publications/practiceguides/.

[54] National Institute of Medicine (2019). Benefits and risks of screening tests. https://www.ncbi.nlm.nih.gov/books/NBK279418/

[55] O’Brien, L., Paul, F., Anderson, D., Hunter, J., Lamb, S., & Sahlberg, P. (2023).   Improving Outcomes for All: The Report of the Independent Expert Panel’s Review to Inform a Better and Fairer Education System. https://www.education.gov.au/review-inform-better-and-fairer-education-system/resources/expert-panels-report

[56] De Bruin, K., Kestel, E., Francis, M., Forgasz, H. & Fries, R. (2023), Supporting students significantly behind in literacy and numeracy: a review of evidence-based approaches. Edresearch.edu.au

aero-supporting-students-significantly-behind-literacy-numeracy.pdf (edresearch.edu.au)

[57] Kovaleski, J.F., VanDerHeyden, A.M., Runge, T.J., Zirkel, P.A., & Shapiro, E.S. (2023). The RTI Approach to Evaluating Learning Disabilities (2nd Edition). Guildford Press.

[58] Jordan, N.C., Glutting, J.J., & Dyson, N. (2012). Number Sense Screener (NSS): User’s guide, K-1, Research Edition. Brookes Publishing Co.

[59] Jordan, N.C. (2024). Stability of early math competencies for predicting math difficulties. Unpublished manuscript.

[60] Jordan, N. C., & Dyson, N. (2014). Number Sense Interventions (1st ed.). Paul H. Brookes Publishing Co.

[61] Aunio, P., & Räsänen, P. (2016). Core numerical skills for learning mathematics in children aged five to eight years – a working model for educators. European Early Childhood Education Research Journal, 24(5), 684–704. https://doi.org/10.1080/1350293X.2014.996424

[62] Lopez-Pederson, A., Mononen, R. Korhonen, J., Aunio, P., & Melby-Lervag, M. (2020). Validation of an early numeracy screener for first Graders. Scandanavian Journal of Educational Research, 65, 404-424.

[63] Hellstrand, H., Korhonen, J., Räsänen, P., Linnanmäki, K., & Aunio, P. (2020). Reliability and validity evidence of the early numeracy test for identifying children at risk for mathematical learning difficulties. International Journal of Educational Research, 102, 101580-. https://doi.org/10.1016/j.ijer.2020.101580

[64] Mononen, R., & Aunio, P. (2016). Counting skills intervention for low-performing first graders. South African Journal of Childhood Education, 6(1), 9–9. https://doi.org/10.4102/sajce.v6i1.407

[65] Gersten, R., Beckmann, S., Clarke, B., Foegen, A., Marsh, L., Star, J. R., & Witzel, B. (2009). Assisting students struggling with mathematics: Response to Intervention (RtI) for elementary and middle schools (NCEE 2009-4060). Washington, DC: National Center for Education Evaluation and Regional Assistance, Institute of Education Sciences, U.S. Department of Education. Retrieved from http://ies. ed.gov/ncee/wwc/publications/practiceguides/.

[66] Purpura, D. J., & Lonigan, C. J. (2015). Early Numeracy Assessment: The Development of the Preschool Early Numeracy Scales. Early Education and Development, 26(2), 286–313. https://doi.org/10.1080/10409289.2015.991084

[67] Van Norman, E. R., Nelson, P. M., Klingbeil, D. A., Cormier, D. C., & Lekwa, A. J. (2019). Gated Screening Frameworks for Academic Concerns: the Influence of Redundant Information on Diagnostic Accuracy Outcomes. California School Psychologist, 23(2), 152–162. https://doi.org/10.1007/s40688-018-0183-0

[68] VanDerHeyden, A. M., Broussard, C., & Burns, M. K. (2021). Classification Agreement for Gated Screening in Mathematics: Subskill Mastery Measurement and Classwide Intervention. Assessment for Effective Intervention, 46(4), 270–280. https://doi.org/10.1177/1534508419882484

[69] Van Norman, E. R., Nelson, P. M., & Klingbeil, D. A. (2017). Single Measure and Gated Screening Approaches for Identifying Students At-Risk for Academic Problems: Implications for Sensitivity and Specificity. School Psychology Quarterly, 32(3), 405–413. https://doi.org/10.1037/spq0000177

[70] Van Norman, E. R., Nelson, P. M., Klingbeil, D. A., Cormier, D. C., & Lekwa, A. J. (2019). Gated Screening Frameworks for Academic Concerns: the Influence of Redundant Information on Diagnostic Accuracy Outcomes. Contemporary School Psychology, 23(2), 152–162. https://doi.org/10.1007/s40688-018-0183-0

[71] Devlin, B. L., Jordan, N. C., & Klein, A. (2022). Predicting mathematics achievement from subdomains of early number competence: Differences by grade and achievement level. Journal of Experimental Child Psychology, 217, 105354–105354. https://doi.org/10.1016/j.jecp.2021.105354

[72] VanDerHeyden, A. M., Broussard, C., & Burns, M. K. (2021). Classification Agreement for Gated Screening in Mathematics: Subskill Mastery Measurement and Classwide Intervention. Assessment for Effective Intervention, 46(4), 270–280. https://doi.org/10.1177/1534508419882484

[73] Compton, D. L., Fuchs, D., Fuchs, L. S., Bouton, B., Gilbert, J. K., Barquero, L. A., Cho, E., & Crouch, R. C. (2010). Selecting At-Risk First-Grade Readers for Early Intervention: Eliminating False Positives and Exploring the Promise of a Two-Stage Gated Screening Process. Journal of Educational Psychology, 102(2), 327–340. https://doi.org/10.1037/a0018448

[74] Van Norman, E. R., Nelson, P. M., & Klingbeil, D. A. (2017). Single Measure and Gated Screening Approaches for Identifying Students At-Risk for Academic Problems: Implications for Sensitivity and Specificity. School Psychology Quarterly, 32(3), 405–413. https://doi.org/10.1037/spq0000177

[75] From p.2 Iragorri, N., Spackman, E. (2018). Assessing the value of screening tools: reviewing the challenges and opportunities of cost-effectiveness analysis. Public Health Review, 39(17), 1-27. https://doi.org/10.1186/s40985-018-0093-8

[76] InformedHealth.org [Internet]. Cologne, Germany: Institute for Quality and Efficiency in Health Care (IQWiG); 2006-. Benefits and risks of screening tests. 2013 Nov 7 [Updated 2019 Dec 17]. Available from: https://www.ncbi.nlm.nih.gov/books/NBK279418/

[77] Fuchs, L. S., & Fuchs, D. (1986). Effects of systematic formative evaluation: A meta-analysis. Exceptional Children, 53(3), 199–208. https://doi.org/10.1177/ 001440298605300301.

[78] Knops, A. (2020). Numerical cognition. Routledge.

[79]National University (2020). Behaviorism in education: What is behavioral learning theory?  https://www.nu.edu/blog/behaviorism-in-education/#:~:text=Overview%20of%20Behavioral%20Learning%20Theory&text=Behaviorists%20proposed%20that%20environmental%20stimuli,behaviors%20based%20on%20their%20outcomes.

[80] Share, D. L. (2021). Common misconceptions about the phonological deficit theory of dyslexia. Brain Sciences, 11(11), 1510-. https://doi.org/10.3390/brainsci11111510

[81] Ehri, L. C., Nunes, S. R., Stahl, S. A., & Willows, D. M. (2001). Systematic Phonics Instruction Helps Students Learn to Read: Evidence from the National Reading Panel’s Meta-Analysis. Review of Educational Research, 71(3), 393–447. https://doi.org/10.3102/00346543071003393

[82] Rose, J. (2006). Independent Review into the Teaching of Early Reading. Department for Education and Skills.

[83] Rowe, K., & National Inquiry into the Teaching of Literacy (Australia). (2005). Teaching Reading: Report and Recommendations. Department of Education, Science and Training. https://research.acer.edu.au/tll_misc/5

[84] Lau, N. T. T., Merkley, R., Tremblay, P., Zhang, S., De Jesus, S., & Ansari, D. (2021). Kindergarteners’ Symbolic Number Abilities Predict Nonsymbolic Number Abilities and Math Achievement in Grade 1. Developmental Psychology, 57(4), 471–488. https://doi.org/10.1037/dev0001158

[85] Dehaene, Stanislas. (2000). Number Sense: How the mind creates mathematics. Oxford University Press.

[86] Siegler, R. S. (2016). Magnitude knowledge: the common core of numerical development. Developmental Science, 19(3), 341–361. https://doi.org/10.1111/desc.12395

[87] Jordan, N. C., Hansen, N., Fuchs, L. S., Siegler, R. S., Gersten, R., & Micklos, D. (2013). Developmental predictors of fraction concepts and procedures. Grantee Submission, 116(1), 45–58. https://doi.org/10.1016/j.jecp.2013.02.001

[88] Tam, Y. P., Wong, T. T.-Y., & Chan, W. W. L. (2019). The relation between spatial skills and mathematical abilities: The mediating role of mental number line representation. Contemporary Educational Psychology, 56, 14–24. https://doi.org/10.1016/j.cedpsych.2018.10.007

[89] Gilligan, K. A., Flouri, E., & Farran, E. K. (2017). The contribution of spatial ability to mathematics achievement in middle childhood. Journal of Experimental Child Psychology, 163, 107–125. https://doi.org/10.1016/j.jecp.2017.04.016

[90] Booth, J. L., & Siegler, R. S. (2008). Numerical Magnitude Representations Influence Arithmetic Learning. Child Development, 79(4), 1016–1031. https://doi.org/10.1111/j.1467-8624.2008.01173.x

[91] Booth, J. L., & Siegler, R. S. (2008). Numerical Magnitude Representations Influence Arithmetic Learning. Child Development, 79(4), 1016–1031. https://doi.org/10.1111/j.1467-8624.2008.01173.x

[92] Devlin, B. L., Jordan, N. C., & Klein, A. (2022). Predicting mathematics achievement from subdomains of early number competence: Differences by grade and achievement level. Journal of Experimental Child Psychology, 217, 105354–105354. https://doi.org/10.1016/j.jecp.2021.105354

[93] Zhang, X., Räsänen, P., Koponen, T., Aunola, K., Lerkkanen, M., & Nurmi, J. (2020). Early Cognitive Precursors of Children’s Mathematics Learning Disability and Persistent Low Achievement: A 5‐Year Longitudinal Study. Child Development, 91(1), 7–27. https://doi.org/10.1111/cdev.13123

[94] Schneider, M., Grabner, R. H., & Paetsch, J. (2009). Mental Number Line, Number Line Estimation, and Mathematical Achievement: Their Interrelations in Grades 5 and 6. Journal of Educational Psychology, 101(2), 359–372. https://doi.org/10.1037/a0013840

[95] Geary, D. C., Nicholas, A., Li, Y., & Sun, J. (2017). Developmental Change in the Influence of Domain-General Abilities and Domain-Specific Knowledge on Mathematics Achievement: An Eight-Year Longitudinal Study. Journal of Educational Psychology, 109(5), 680–693. https://doi.org/10.1037/edu0000159

[96] Haring, N. G., & Eaton, M. D. (1978). Systematic instructional procedures: An instructional hierarchy. In N. G. Haring, T. C. Lovitt, M. D. Eaton, & C. L. Hansen (Eds.), The fourth R: Research in the classroom (pp. 23–40). Merrill.

[97] Codding, R. S., Nelson, G., Kiss, A. J., Shin, J., Goodridge, A., & Hwang, J. (2023). A Meta-Analysis of the Relations Between Curriculum-Based Measures in Mathematics and Criterion Measures. School Psychology Review, ahead-of-print(ahead-of-print), 1–16. https://doi.org/10.1080/2372966X.2023.2224055

[98] VanDerHeyden, A. M., Broussard, C., & Burns, M. K. (2021). Classification Agreement for Gated Screening in Mathematics: Subskill Mastery Measurement and Classwide Intervention. Assessment for Effective Intervention, 46(4), 270–280. https://doi.org/10.1177/1534508419882484

[100] Solomon, B. G., VanDerHeyden, A. M., Solomon, E. C., Korzeniewski, E. R., Payne, L. L., Campaña, K. V., & Dillon, C. R. (2022). Mastery Measurement in Mathematics and the Goldilocks Effect. School Psychology, 37(3), 213–224. https://doi.org/10.1037/spq0000496

[101] VanDerHeyden, A. M., Broussard, C., & Burns, M. K. (2021). Classification Agreement for Gated Screening in Mathematics: Subskill Mastery Measurement and Classwide Intervention. Assessment for Effective Intervention, 46(4), 270–280. https://doi.org/10.1177/1534508419882484

[102] VanDerHeyden, A. M., & Broussard, C. (2021). Construction and Examination of Math Subskill Mastery Measures. Assessment for Effective Intervention, 46(3), 188–196. https://doi.org/10.1177/1534508419883947

[103] Cross, C. T., Woods, T. A., & Schweingruber, H. A. (2009). Mathematics learning in early childhood paths toward excellence and equity. National Academies Press.

[104] Milburn, T. F., Lonigan, C. J., DeFlorio, L., & Klein, A. (2019). Dimensionality of preschoolers’ informal mathematical abilities. Early Childhood Research Quarterly, 47, 487–495. https://doi.org/10.1016/j.ecresq.2018.07.006

[105] Purpura, D. J., & Lonigan, C. J. (2013). Informal Numeracy Skills: The Structure and Relations Among Numbering, Relations, and Arithmetic Operations in Preschool. American Educational Research Journal, 50(1), 178–209. https://doi.org/10.3102/0002831212465332

[106] Buckingham, J., Nayton, M., Snow, P., Capp, S., Prince, G., McNamara, A. (2017). National Year 1 Literacy and Numeracy Check. Expert Advisory Panel: Advice to the Minister. https://apo.org.au/sites/default/files/resource-files/2017-09/apo-nid107126_1.pdf

[107] Berch, D. B. (2005). Making sense of number sense: Implications for children with Mathematical Disabilities. Journal of Learning Disabilities, 38(4), 333–339. https://doi.org/10.1177/00222194050380040901

[108] Nelson, G., Kiss, A. J., Codding, R. S., McKevett, N. M., Schmitt, J. F., Park, S., Romero, M. E., & Hwang, J. (2023). Review of curriculum-based measurement in mathematics: An update and extension of the literature. Journal of School Psychology, 97, 1–42. https://doi.org/10.1016/j.jsp.2022.12.001

[109] Ruiz, C., Kohnen, S., von Hagen, A., Kwok, F. Y., & Bull, R. (2024). Which domain-specific skills at the beginning of formal schooling predict later mathematical achievement? A systematic review and meta-analysis. Educational Research Review, 42, 100583-. https://doi.org/10.1016/j.edurev.2023.100583

[110] Nguyen, T., Watts, T. W., Duncan, G. J., Clements, D. H., Sarama, J. S., Wolfe, C., & Spitler, M. E. (2016). Which preschool mathematics competencies are most predictive of fifth grade achievement? Early Childhood Research Quarterly, 36, 550–560.

[111] Le, M.-L., & Noel, M.-P. (2021). Preschoolers’ mastery of advanced counting: The best predictor of addition skills 2 years later. Journal of Experimental Child Psychology, 212, 105252–105252. https://doi.org/10.1016/j.jecp.2021.105252

[112] Nelson, G., Kiss, A. J., Codding, R. S., McKevett, N. M., Schmitt, J. F., Park, S., Romero, M. E., & Hwang, J. (2023). Review of curriculum-based measurement in mathematics: An update and extension of the literature. Journal of School Psychology, 97, 1–42. https://doi.org/10.1016/j.jsp.2022.12.001

[113] Ruiz, C., Kohnen, S., von Hagen, A., Kwok, F. Y., & Bull, R. (2024). Which domain-specific skills at the beginning of formal schooling predict later mathematical achievement? A systematic review and meta-analysis. Educational Research Review, 42, 100583-. https://doi.org/10.1016/j.edurev.2023.100583

[114] Nogues, C. P., & Dorneles, B. V. (2021). Systematic review on the precursors of initial mathematical performance. International Journal of Educational Research Open, 2, 100035-. https://doi.org/10.1016/j.ijedro.2021.100035

[115] Nogues, C. P., & Dorneles, B. V. (2021). Systematic review on the precursors of initial mathematical performance. International Journal of Educational Research Open, 2, 100035-. https://doi.org/10.1016/j.ijedro.2021.100035

[116] Nelson, G., Kiss, A. J., Codding, R. S., McKevett, N. M., Schmitt, J. F., Park, S., Romero, M. E., & Hwang, J. (2023). Review of curriculum-based measurement in mathematics: An update and extension of the literature. Journal of School Psychology, 97, 1–42. https://doi.org/10.1016/j.jsp.2022.12.001

[117] Nogues, C. P., & Dorneles, B. V. (2021). Systematic review on the precursors of initial mathematical performance. International Journal of Educational Research Open, 2, 100035-. https://doi.org/10.1016/j.ijedro.2021.100035

[118] Schneider, M. Beeres, K. Coban, L., Merz, S., Schmidt, S., Stricker, J. et a; (2017) Associations of non-symbolic and symbolic numerical magnitude processing with mathematical competence: A meta-analysis. Developmental Science, 20(3), Article e12372.

[119] Schneider, M, Merz, S., Stricker. J., De Smedt, B., Torbeyns, J., Verschaffel, L. et al (2018). Associations of number line estimations with mathematical competence: A meta-analysis. Child Development, 89(5), 1467-1484.

[120] Jordan, N. C., Kaplan, D., Locuniak, M. N., & Ramineni, C. (2007). Predicting First-Grade Math Achievement from Developmental Number Sense Trajectories. Learning Disabilities Research and Practice, 22(1), 36–46. https://doi.org/10.1111/j.1540-5826.2007.00229.x

[121] Jordan, N. C., Kaplan, D., Nabors Oláh, L., & Locuniak, M. N. (2006). Number Sense Growth in Kindergarten: A Longitudinal Investigation of Children at Risk for Mathematics Difficulties. Child Development, 77(1), 153–175. https://doi.org/10.1111/j.1467-8624.2006.00862.x

[122] Hornung, C., Schiltz, C., Brunner, M., & Martin, R. (2014). Predicting first-grade mathematics achievement: the contributions of domain-general cognitive abilities, nonverbal number sense, and early number competence. Frontiers in Psychology, 5, 272–272. https://doi.org/10.3389/fpsyg.2014.00272

[123] Nelson, G., Kiss, A. J., Codding, R. S., McKevett, N. M., Schmitt, J. F., Park, S., Romero, M. E., & Hwang, J. (2023). Review of curriculum-based measurement in mathematics: An update and extension of the literature. Journal of School Psychology, 97, 1–42. https://doi.org/10.1016/j.jsp.2022.12.001

[124] Ruiz, C., Kohnen, S., von Hagen, A., Kwok, F. Y., & Bull, R. (2024). Which domain-specific skills at the beginning of formal schooling predict later mathematical achievement? A systematic review and meta-analysis. Educational Research Review, 42, 100583-. https://doi.org/10.1016/j.edurev.2023.100583

[125] Jordan, N. C., Devlin, B. L., & Botello, M. (2022). Core foundations of early mathematics: refining the number sense framework. Current Opinion in Behavioral Sciences, 46, 101181-. https://doi.org/10.1016/j.cobeha.2022.101181

[126] Van Der Heyden, A. M., Codding, R. S., & Martin, R. (2017). Relative value of common screening measures in mathematics. School Psychology Review, 46(1), 65–87. https://doi.org/10.17105/SPR46-1.65-87

[127] Sutherland, M., Clarke, B., Nese, J. F. T., Strand Cary, M., Shanley, L., Furjanic, D., & Durán, L. (2021). Investigating the utility of a kindergarten number line assessment compared to an early numeracy screening battery. Early Childhood Research Quarterly, 55, 119–128. https://doi.org/10.1016/j.ecresq.2020.11.003

[128] VanDerHeyden, A., McLaughlin, T., Algina, J., & Snyder, P. (2012). Randomized evaluation of a supplemental grade-wide mathematics intervention. American Educational Research Journal, 49(6), 1251–1284. https://doi.org/10.3102/0002831212462736

[129] Nelson, G., Kiss, A. J., Codding, R. S., McKevett, N. M., Schmitt, J. F., Park, S., Romero, M. E., & Hwang, J. (2023). Review of curriculum-based measurement in mathematics: An update and extension of the literature. Journal of School Psychology, 97, 1–42. https://doi.org/10.1016/j.jsp.2022.12.001

[130] Devlin, B. L., Jordan, N. C., & Klein, A. (2022). Predicting mathematics achievement from subdomains of early number competence: Differences by grade and achievement level. Journal of Experimental Child Psychology, 217, 105354–105354. https://doi.org/10.1016/j.jecp.2021.105354

[131] Geary, D. C., Nicholas, A., Li, Y., & Sun, J. (2017). Developmental Change in the Influence of Domain-General Abilities and Domain-Specific Knowledge on Mathematics Achievement: An Eight-Year Longitudinal Study. Journal of Educational Psychology, 109(5), 680–693. https://doi.org/10.1037/edu0000159

[132] Ribner, A. D., Ahmed, S. F., Miller-Cotto, D., & Ellis, A. (2023). The role of executive function in shaping the longitudinal stability of math achievement during early elementary grades. Early Childhood Research Quarterly, 64, 84–93. https://doi.org/10.1016/j.ecresq.2023.02.004

[133] Geary, D. C. (2011). Cognitive predictors of achievement growth in mathematics: A 5-year longitudinal study. Developmental Psychology, 47(6), 1539–1552. https://doi.org/10.1037/a0025510

[134] Jordan, N. C., Devlin, B. L., & Botello, M. (2022). Core foundations of early mathematics: refining the number sense framework. Current Opinion in Behavioral Sciences, 46, 101181-. https://doi.org/10.1016/j.cobeha.2022.101181

[135] Nogues, C. P., & Dorneles, B. V. (2021). Systematic review on the precursors of initial mathematical performance. International Journal of Educational Research Open, 2, 100035-. https://doi.org/10.1016/j.ijedro.2021.100035

[136] Vanderheyden, A. M., & Solomon, B. G. (2023). Valid Outcomes for Screening and Progress Monitoring: Fluency Is Superior to Accuracy in Curriculum-Based Measurement. School Psychology, 38(3), 160–172. https://doi.org/10.1037/spq0000528

[137] Vanderheyden, A. M., & Solomon, B. G. (2023). Valid Outcomes for Screening and Progress Monitoring: Fluency Is Superior to Accuracy in Curriculum-Based Measurement. School Psychology, 38(3), 160–172. https://doi.org/10.1037/spq0000528

[138] Landerl, K., Bevan, A., & Butterworth, B. (2004). Developmental dyscalculia and basic numerical capacities: a study of 8–9-year-old students. Cognition, 93(2), 99–125. https://doi.org/10.1016/j.cognition.2003.11.004

[139] Geary, D. C., Hoard, M. K., Byrd-Craven, J., & Catherine DeSoto, M. (2004). Strategy choices in simple and complex addition: Contributions of working memory and counting knowledge for children with mathematical disability. Journal of Experimental Child Psychology, 88(2), 121–151. https://doi.org/10.1016/j.jecp.2004.03.002

[140] p. 39 of Ginsburg, H. (1997). Entering the child’s mind : the clinical interview in psychological research and practice. Cambridge University Press.

[141] Kaskens, J., Goei, S. L., Van Luit, J. E. H., Verhoeven, L., & Segers, E. (2022). Dynamic maths interviews to identify educational needs of students showing low math achievement. European Journal of Special Needs Education, 37(3), 432–446. https://doi.org/10.1080/08856257.2021.1889848 https://librarysearch.murdoch.edu.au/permalink/61MUN_INST/1c1bmht/cdi_informaworld_taylorfrancis_310_1080_08856257_2021_1889848

[142] Ginsburg, H. P., Lee, Y.-S., & Pappas, S. (2016). A research-inspired and computer-guided clinical interview for mathematics assessment: introduction, reliability and validity. ZDM, 48(7), 1003–1018. https://doi.org/10.1007/s11858-016-0794-8

[143] Higgins, J., & Bonne, L. (2008). The Role of the Diagnostic Interview in the Numeracy Development Projects. Findings from the New Zealand Numeracy Development Projects https://nzmaths.co.nz/sites/default/files/Numeracy/References/Comp08/comp08_higgins_bonne_3.pdf

[144] Jenkins, O. F. (2010). Developing teachers’ knowledge of students as learners of mathematics through structured interviews. Journal of Mathematics Teacher Education, 13(2), 141–154. https://doi.org/10.1007/s10857-009-9129-9

[145] Schack, E. O., Fisher, M. H., Thomas, J. N., Eisenhardt, S., Tassell, J., & Yoder, M. (2013). Prospective elementary school teachers’ professional noticing of children’s early numeracy. Journal of Mathematics Teacher Education, 16(5), 379–397. https://doi.org/10.1007/s10857-013-9240-9

[146] Devlin, B. L., Jordan, N. C., & Klein, A. (2022). Predicting mathematics achievement from subdomains of early number competence: Differences by grade and achievement level. Journal of Experimental Child Psychology, 217, 105354–105354. https://doi.org/10.1016/j.jecp.2021.105354

[147] Fogarty, G. (2007). Research on the Progressive Achievement Tests and Academic Achievement in Schools. Australian Council for Educational Research (ACER). https://research.acer.edu.au/ar_misc/45

[148] Gersten, R., Clarke, B., Jordan, N. C., Newman-Gonchar, R., Haymond, K., & Wilkins, C. (2012) 441. Universal Screening in Mathematics for the Primary Grades: Beginnings of a Research Base. Exceptional Children, 78(4), 423–445. https://doi.org/10.1177/001440291207800403

[149] Geary, D. (in press). The evolved mind and modern education: Status of evolutionary educational psychology. Cambridge University Press.

[150] Jordan, N. C., Glutting, J., Dyson, N., Hassinger-Das, B., & Irwin, C. (2012). Building kindergartners’ number sense: A randomized controlled study. Journal of Educational Psychology, 104(3), 647–660. https://doi.org/10.1037/a0029018

[151] Sterner, G., Wolff, U., & Helenius, O. (2020). Reasoning about representations: Effects of an early math intervention. Scandinavian Journal of Educational Research, 64(5), 782–800. https://doi.org/10.1080/00313831.2019.1600579

[152] Cooper, S., Shelton, R. N., Padgett, R. N., Crowley, B., Kerschen, K., & Donham, M. P. (2022). The impact of a Summer intervention focused on foundational concepts of number sense for early learners. Investigations in Mathematics Learning, 14(3), 199–214. https://doi.org/10.1080/19477503.2022.2073120

[153] Doabler, C. T., Clarke, B., Kosty, D., Smolkowski, K., Kurtz-Nelson, E., Fien, H., & Baker, S. K. (2019). Building number sense among English learners: A multisite randomized controlled trial of a Tier 2 kindergarten mathematics intervention. Early Childhood Research Quarterly, 47, 432–444. https://doi.org/10.1016/j.ecresq.2018.08.004

[154] Chiara Passolunghi, M., & Lanfranchi, S. (2012). Domain-specific and domain-general precursors of mathematical achievement: A longitudinal study from kindergarten to first grade : Mathematical and cognitive predictors of the development of mathematics. British Journal of Educational Psychology, 82, 42–63.

[155] Jordan, Glutting & Ramineni (2010). The importance of number sense to mathematics achievement in first to third grades. Learning and Individual Differences, 20(2), 82-88.

[156] Allen, K., Giofrè, D., Higgins, S., & Adams, J. (2021). Using working memory performance to predict mathematics performance 2 years on. Psychological Research, 85(5), 1986–1996. https://doi.org/10.1007/s00426-020-01382-5

[157] Peng, P., Namkung, J., Barnes, M., & Sun, C. (2016). A Meta-Analysis of Mathematics and Working Memory: Moderating Effects of Working Memory Domain, Type of Mathematics Skill, and Sample Characteristics. Journal of Educational Psychology, 108(4), 455–473. https://doi.org/10.1037/edu0000079

[158] Hassinger-Das, B., Jordan, N. C., Glutting, J., Irwin, C., & Dyson, N. (2014). Domain-general mediators of the relation between kindergarten number sense and first-grade mathematics achievement. Journal of Experimental Child Psychology, 118, 78–92. https://doi.org/10.1016/j.jecp.2013.09.008

[159] Möhring, W., Ribner, A. D., Segerer, R., Libertus, M. E., Kahl, T., Troesch, L. M., & Grob, A. (2021). Developmental trajectories of children’s spatial skills: Influencing variables and associations with later mathematical thinking. Learning and Instruction, 75, 101515-. https://doi.org/10.1016/j.learninstruc.2021.101515

[160] Hornung, C., Schiltz, C., Brunner, M., & Martin, R. (2014). Predicting first-grade mathematics achievement: the contributions of domain-general cognitive abilities, nonverbal number sense, and early number competence. Frontiers in Psychology, 5, 272–272. https://doi.org/10.3389/fpsyg.2014.0

[161] Ribner, A. D. (2020). Executive function facilitates learning from math instruction in kindergarten: Evidence from the ECLS-K. Learning and Instruction, 65, 101251-. https://doi.org/10.1016/j.learninstruc.2019.101251

[162] Alloway, T. P. (2014). Understanding working memory (2nd edition.). SAGE Publications.

[163] Möhring, W., Ribner, A. D., Segerer, R., Libertus, M. E., Kahl, T., Troesch, L. M., & Grob, A. (2021). Developmental trajectories of children’s spatial skills: Influencing variables and associations with later mathematical thinking. Learning and Instruction, 75, 101515-. https://doi.org/10.1016/j.learninstruc.2021.101515

[164] Judd, N., & Klingberg, T. (2021). Training spatial cognition enhances mathematical learning in a randomized study of 17,000 children. Nature Human Behaviour, 5(11), 1548–1554. https://doi.org/10.1038/s41562-021-01118-4

[165] Tam, Y. P., Wong, T. T.-Y., & Chan, W. W. L. (2019). The relation between spatial skills and mathematical abilities: The mediating role of mental number line representation. Contemporary Educational Psychology, 56, 14–24. https://doi.org/10.1016/j.cedpsych.2018.10.007

[166] Koponen, T., Georgiou, G., Salmi, P., Leskinen, M., & Aro, M. (2017). A Meta-Analysis of the Relation Between RAN and Mathematics. Journal of Educational Psychology, 109(7), 977–992. https://doi.org/10.1037/edu0000182

[167] Zhang, X., Räsänen, P., Koponen, T., Aunola, K., Lerkkanen, M., & Nurmi, J. (2020). Early Cognitive Precursors of Children’s Mathematics Learning Disability and Persistent Low Achievement: A 5‐Year Longitudinal Study. Child Development, 91(1), 7–27. https://doi.org/10.1111/cdev.13123

[168] Jordan, N. C., & Levine, S. C. (2009). Socioeconomic variation, number competence, and mathematics learning difficulties in young children. Developmental Disabilities Research Reviews, 15(1), 60–68. https://doi.org/10.1002/ddrr.46

[169] Dowker A. (2005). Individual differences in arithmetic: implications for psychology, neuro-science, and education. Hove and NY: Psychology Press.

[170] Jordan NC, Levine SC, Huttenlocher J. (1994).Development of calculation abilities in middle- and low-income children after formal instruction in school. Journal of Applied Developmental Psychology, 15, 223–240

[171] Hornburg, C. B., Schmitt, S. A., & Purpura, D. J. (2018). Relations between preschoolers’ mathematical language understanding and specific numeracy skills. Journal of Experimental Child Psychology, 176, 84–100. https://doi.org/10.1016/j.jecp.2018.07.005

[172] Purpura, D. J., Napoli, A. R., Wehrspann, E. A., & Gold, Z. S. (2017). Causal Connections Between Mathematical Language and Mathematical Knowledge: A Dialogic Reading Intervention. Journal of Research on Educational Effectiveness, 10(1), 116–137. https://doi.org/10.1080/19345747.2016.1204639

[173] Toll, S. W. M., & Van Luit, J. E. H. (2014). The Developmental Relationship Between Language and Low Early Numeracy Skills Throughout Kindergarten. Exceptional Children, 81(1), 64–78. https://doi.org/10.1177/0014402914532233

[174] Lewis, K. E., & Fisher, M. B. (2018). Clinical Interviews: Assessing and Designing Mathematics Instruction for Students With Disabilities. Intervention in School and Clinic, 53(5), 283–291. https://doi.org/10.1177/1053451217736864

[175] Hernandez-Nuhfer, M. P., Poncy, B. C., Duhon, G., Solomon, B. G., & Skinner, C. H. (2020). Factors Influencing the Effectiveness of Interventions: An Interaction of Instructional Set Size and Dose. School Psychology Review, 49(4), 386–398. https://doi.org/10.1080/2372966X.2020.1777832

[176] Codding, R. S., VanDerHeyden, A. M., Martin, R. J., Desai, S., Allard, N., & Perrault, L. (2016). Manipulating Treatment Dose: Evaluating the Frequency of a Small Group Intervention Targeting Whole Number Operations. Learning Disabilities Research and Practice, 31(4), 208–220. https://doi.org/10.1111/ldrp.12120

[177] Center on Multi-Tiered Systems of Supports at the American Institute for Research (2024). Tips for intensifying instruction at tier 1. https://mtss4success.org/resource/tips-intensifying-instruction-tier-1

[178] Mellard, D., McKnight, M., & Jordan, J. (2010). RTI Tier Structures and Instructional Intensity. Learning Disabilities Research and Practice, 25(4), 217–225. https://doi.org/10.1111/j.1540-5826.2010.00319.x

[179] Van Camp, A. M., Wehby, J. H., Martin, B. L. N., Wright, J. R., & Sutherland, K. S. (2020). Increasing Opportunities to Respond to Intensify Academic and Behavioral Interventions: A Meta-Analysis. School Psychology Review, 49(1), 31–46. https://doi.org/10.1080/2372966X.2020.1717369

[180] Fuchs, D., Fuchs, L. S., & Abramson, R. (n.d.). Peer-Assisted Learning Strategies (PALS): A Validated Classwide Program for Improving Reading and Mathematics Performance. In Student Engagement (pp. 109–120). Springer International Publishing. https://doi.org/10.1007/978-3-030-37285-9_6

[181] Fuchs, L. S., Fuchs, D., & Malone, A. S. (2017). The Taxonomy of Intervention Intensity. Teaching Exceptional Children, 50(1), 35–43. https://doi.org/10.1177/0040059917703962

[182] Center on Multi-Tiered Systems of Supports at the American Institute for Research (2024). Tips for intensifying instruction at tier 1. https://mtss4success.org/resource/tips-intensifying-instruction-tier-1

[183] Fuchs, L. S. (2004). The Past, Present, and Future of Curriculum-Based Measurement Research. School Psychology Review, 33(2), 188–192. https://doi.org/10.1080/02796015.2004.12086241

[184] Fuchs, L. S. (2004). The Past, Present, and Future of Curriculum-Based Measurement Research. School Psychology Review, 33(2), 188–192. https://doi.org/10.1080/02796015.2004.12086241

[185] Bailey, D. H., Watts, T. W., Littlefield, A. K., & Geary, D. C. (2014). State and Trait Effects on Individual Differences in Children’s Mathematical Development. Psychological Science, 25(11), 2017–2026. https://doi.org/10.1177/0956797614547539

[186] Bailey, D. H., Fuchs, L. S., Gilbert, J. K., Geary, D. C., & Fuchs, D. (2018). Prevention: Necessary but Insufficient?: A Two-Year Follow-Up of Effective First-Grade Mathematics Intervention. Child Development. https://doi.org/10.1111/cdev.13175

[187] Clements, D. H., Sarama, J., Layzer, C., & Unlu, F. (2023). Implementation of a Scale-Up Model in Early Childhood: Long-Term Impacts on Mathematics Achievement. Journal for Research in Mathematics Education, 54(1), 64–88. https://doi.org/10.5951/jresematheduc-2020-0245

[188] National Mathematics Advisory Panel (2008). Foundations for Success: The Final Report of the National Mathematics Advisory Panel. U.S. Department of Education: Washington, DC.

[189] Siegler, R. S., Duncan, G. J., Davis-Kean, P. E., Duckworth, K., Claessens, A., Engel, M., Susperreguy, M. I., & Chen, M. (2012). Early Predictors of High School Mathematics Achievement. Psychological Science, 23(7), 691–697. https://doi.org/10.1177/0956797612440101

[190] Bailey, D. H., Duncan, G. J., Cunha, F., Foorman, B. R., & Yeager, D. S. (2020) 66. Persistence and Fade-Out of Educational-Intervention Effects: Mechanisms and Potential Solutions. Psychological Science in the Public Interest, 21(2), 55–97. https://doi.org/10.1177/1529100620915848

[191] Williams, L., Groves, O., Wan, W.-Y., Lee, E., & Lu, L. (2023). Learning outcomes of students with early low NAPLAN performance. Australian Education Research Organisation. https://www.edresearch.edu.au/ resources/learning-outcomes-students-early-low-naplan-performance